Convertir desde Binario (Base 2) a Romano (Rom)
Realiza la conversión de números entre los distintos sistemas numéricos.
Binario (Base 2) = Romano (Rom)
Información sobre las unidades de conversión:
Acerca de Binario (Base 2)
El sistema binario es una técnica de numeración donde solo se utilizan dos dígitos, el 0 y el 1. Suele emplearse particularmente en la informática. Es decir, este método se vale solo de dos símbolos, la unidad y el cero. Cualquier número puede expresarse tanto en el sistema decimal como en el binario.
Acerca de Romano (Rom)
El sistema romano es un sistema numérico antiguo que se utilizaba en el Imperio Romano. En este sistema se emplean letras para representar los números, siendo las letras más utilizadas son I, V, X, L, C, D y M. Cada letra tiene un valor numérico específico y se combinan de ciertas maneras para formar los números. A diferencia del sistema decimal, el sistema romano no tiene una representación nativa de la cifra cero. Es decir, no existe un símbolo específico para el cero en el sistema romano. A pesar de esto, el sistema romano sigue siendo utilizado en algunos contextos, como la numeración de los años en algunos calendarios.
Binario (Base 2) vs Romano (Rom)
| Binario (Base 2) | Decimal (Base 10) | Romano (Rom) |
|---|---|---|
| 1 | 1 | I |
| 100 | 4 | IV |
| 101 | 5 | V |
| 1001 | 9 | IX |
| 1010 | 10 | X |
| 101000 | 40 | XL |
| 110010 | 50 | L |
| 1011010 | 90 | XC |
| 1100100 | 100 | C |
| 110010000 | 400 | CD |
| 111110100 | 500 | D |
| 1110000100 | 900 | CM |
| 1111101000 | 1000 | M |
| 111110100000 | 4000 | IV |
| 1001110001000 | 5000 | V |
| 10001100101000 | 9000 | IX |
| 10011100010000 | 10000 | X |
| 1001110001000000 | 40000 | XL |
| 1100001101010000 | 50000 | L |
| 10101111110010000 | 90000 | XC |
| 11000011010100000 | 100000 | C |
| 1100001101010000000 | 400000 | CD |
| 1111010000100100000 | 500000 | D |
| 11011011101110100000 | 900000 | CM |
| 11110100001001000000 | 1000000 | M |
¿Cómo se convierte de Binario (Base 2) a Romano (Rom)?
Nota: Para convertir un número en binario (base 2) a cualquier otra base, primero debemos convertir el valor binario a base decimal (base 10), para ello debemos realizar los siguientes pasos:
- Identifique cada dígito del número binario.
- Calcule la posición de cada dígito. Empiece desde el dígito más a la derecha, que tendrá una posición de 0. Cada dígito a la izquierda tendrá una posición incremental de 1 (1, 2, 3, etc.).
- Calcule el valor decimal de cada dígito multiplicándolo por la base (2) elevada a la posición del dígito. Por ejemplo: dígito * 2^posición.
- Sume los valores obtenidos en el paso anterior para obtener el número decimal equivalente.
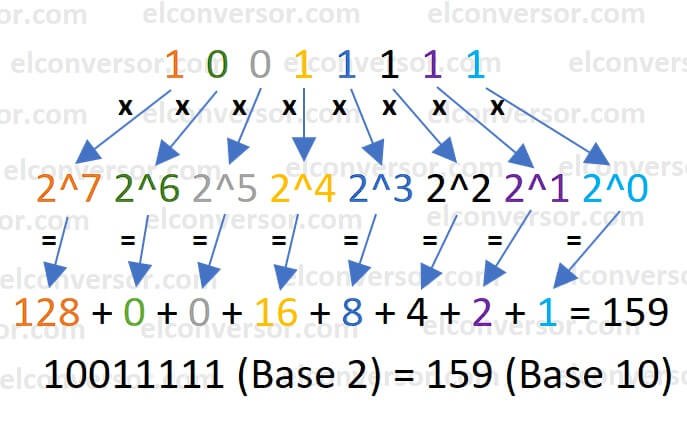
Aplicando estos pasos al número 10011111 binario:
Vamos a ver como pasar el numero binario 10011111 a decimal.
- 1, 0, 0, 1, 1, 1, 1 y 1 son los dígitos.
- Desde el más a la derecha, la posición es 0, 1, 2, 3, 4, 5, 6 y 7.
- 1 * 2^7 = 128; 0 * 2^6 = 0; 0 * 2^5 = 0; 1 * 2^4 = 16; 1 * 2^3 = 8; 1 * 2^2 = 4; 1 * 2^1 = 2; 1 * 2^0 = 1;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 decimal.
Entonces, 10011111 binario = 159 decimal.
Para pasar el numero decimal a número romano debemos de seguir una serie de reglas:
Números romanos y sus reglas básicas.
- Los números romanos I, X, C y M pueden repetirse hasta tres veces a la hora de escribir un número romano compuesto.
- Los números romanos V, L y D no pueden repetirse nunca.
- Si un número romano compuesto tiene un número a la derecha menor que el de la izquierda entonces se suman ambos. Ejemplo: XI: el número de la derecha (I = 1) es menor que el de la izquierda (X = 10) entonces se suman, es decir XI = 11.
- Si un número romano compuesto tiene un número a la derecha mayor que el de la izquierda y éste es un I, X o C, entonces se resta el de la izquierda al derecha. Ejemplo: IX: el número de la derecha (X = 10) es mayor que el de la izquierda (I = 1) y además este es I luego se resta el de la izquierda al de la derecha, es decir IX = 9.
- Si un número romano tiene sobre él una raya, entonces su valor se multiplica por mil. Ejemplo: IX
: el número es 9.000 puesto que es el número romano que representa al 9 y al estar con la raya sobre él se multiplica por mil.
Pasos para convertir el número decimal 159 en número romano:
- Descomponer el número en unidades, en este caso: 100, 50 y 9.
- Traducir usando la tabla, cada número decimal por su equivalente número romano. en este caso: C=100, L=50 y IX=9.
- Escribimos el resultado de mayor a menor unidad o de izquierda a derecha: CLIX.
Como resultado podemos decir que el número decimal 159 es igual a CLIX en número romano.
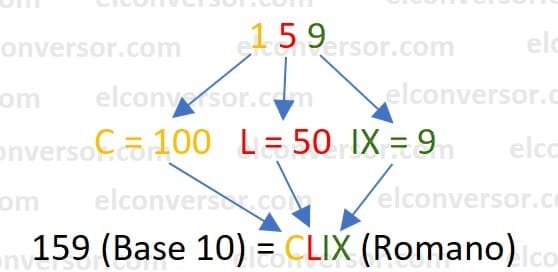
Tabla de conversión de Binario (Base 2) a Romano (Rom)
| Binario (Base 2) | Romano (Rom) |
|---|---|
| 1 | I |
| 10 | II |
| 11 | III |
| 100 | IV |
| 101 | V |
| 110 | VI |
| 111 | VII |
| 1000 | VIII |
| 1001 | IX |
| 1010 | X |
| 1011 | XI |
| 1100 | XII |
| 1101 | XIII |
| 1110 | XIV |
| 1111 | XV |
| 10000 | XVI |
| 10001 | XVII |
| 10010 | XVIII |
| 10011 | XIX |
| 10100 | XX |
| 10101 | XXI |
| 10110 | XXII |
| 10111 | XXIII |
| 11000 | XXIV |
| 11001 | XXV |
| 11010 | XXVI |
| 11011 | XXVII |
| 11100 | XXVIII |
| 11101 | XXIX |
| 11110 | XXX |
| 11111 | XXXI |
| 100000 | XXXII |
| 100001 | XXXIII |
| 100010 | XXXIV |
| 100011 | XXXV |
| 100100 | XXXVI |
| 100101 | XXXVII |
| 100110 | XXXVIII |
| 100111 | XXXIX |
| 101000 | XL |
| 101001 | XLI |
| 101010 | XLII |
| 101011 | XLIII |
| 101100 | XLIV |
| 101101 | XLV |
| 101110 | XLVI |
| 101111 | XLVII |
| 110000 | XLVIII |
| 110001 | XLIX |
| 110010 | L |
| 110011 | LI |
| 110100 | LII |
| 110101 | LIII |
| 110110 | LIV |
| 110111 | LV |
| 111000 | LVI |
| 111001 | LVII |
| 111010 | LVIII |
| 111011 | LIX |
| 111100 | LX |
| 111101 | LXI |
| 111110 | LXII |
| 111111 | LXIII |
| 1000000 | LXIV |
| 1000001 | LXV |
| 1000010 | LXVI |
| 1000011 | LXVII |
| 1000100 | LXVIII |
| 1000101 | LXIX |
| 1000110 | LXX |
| 1000111 | LXXI |
| 1001000 | LXXII |
| 1001001 | LXXIII |
| 1001010 | LXXIV |
| 1001011 | LXXV |
| 1001100 | LXXVI |
| 1001101 | LXXVII |
| 1001110 | LXXVIII |
| 1001111 | LXXIX |
| 1010000 | LXXX |
| 1010001 | LXXXI |
| 1010010 | LXXXII |
| 1010011 | LXXXIII |
| 1010100 | LXXXIV |
| 1010101 | LXXXV |
| 1010110 | LXXXVI |
| 1010111 | LXXXVII |
| 1011000 | LXXXVIII |
| 1011001 | LXXXIX |
| 1011010 | XC |
| 1011011 | XCI |
| 1011100 | XCII |
| 1011101 | XCIII |
| 1011110 | XCIV |
| 1011111 | XCV |
| 1100000 | XCVI |
| 1100001 | XCVII |
| 1100010 | XCVIII |
| 1100011 | XCIX |
| 1100100 | C |
| 1100101 | CI |
| 1100110 | CII |
| 1100111 | CIII |
| 1101000 | CIV |
| 1101001 | CV |
| 1101010 | CVI |
| 1101011 | CVII |
| 1101100 | CVIII |
| 1101101 | CIX |
| 1101110 | CX |
| 1101111 | CXI |
| 1110000 | CXII |
| 1110001 | CXIII |
| 1110010 | CXIV |
| 1110011 | CXV |
| 1110100 | CXVI |
| 1110101 | CXVII |
| 1110110 | CXVIII |
| 1110111 | CXIX |
| 1111000 | CXX |
| 1111001 | CXXI |
| 1111010 | CXXII |
| 1111011 | CXXIII |
| 1111100 | CXXIV |
| 1111101 | CXXV |
| 1111110 | CXXVI |
| 1111111 | CXXVII |
| 10000000 | CXXVIII |
| 10000001 | CXXIX |
| 10000010 | CXXX |
| 10000011 | CXXXI |
| 10000100 | CXXXII |
| 10000101 | CXXXIII |
| 10000110 | CXXXIV |
| 10000111 | CXXXV |
| 10001000 | CXXXVI |
| 10001001 | CXXXVII |
| 10001010 | CXXXVIII |
| 10001011 | CXXXIX |
| 10001100 | CXL |
| 10001101 | CXLI |
| 10001110 | CXLII |
| 10001111 | CXLIII |
| 10010000 | CXLIV |
| 10010001 | CXLV |
| 10010010 | CXLVI |
| 10010011 | CXLVII |
| 10010100 | CXLVIII |
| 10010101 | CXLIX |
| 10010110 | CL |
| 10010111 | CLI |
| 10011000 | CLII |
| 10011001 | CLIII |
| 10011010 | CLIV |
| 10011011 | CLV |
| 10011100 | CLVI |
| 10011101 | CLVII |
| 10011110 | CLVIII |
| 10011111 | CLIX |
| 10100000 | CLX |
| 10100001 | CLXI |
| 10100010 | CLXII |
| 10100011 | CLXIII |
| 10100100 | CLXIV |
| 10100101 | CLXV |
| 10100110 | CLXVI |
| 10100111 | CLXVII |
| 10101000 | CLXVIII |
| 10101001 | CLXIX |
| 10101010 | CLXX |
| 10101011 | CLXXI |
| 10101100 | CLXXII |
| 10101101 | CLXXIII |
| 10101110 | CLXXIV |
| 10101111 | CLXXV |
| 10110000 | CLXXVI |
| 10110001 | CLXXVII |
| 10110010 | CLXXVIII |
| 10110011 | CLXXIX |
| 10110100 | CLXXX |
| 10110101 | CLXXXI |
| 10110110 | CLXXXII |
| 10110111 | CLXXXIII |
| 10111000 | CLXXXIV |
| 10111001 | CLXXXV |
| 10111010 | CLXXXVI |
| 10111011 | CLXXXVII |
| 10111100 | CLXXXVIII |
| 10111101 | CLXXXIX |
| 10111110 | CXC |
| 10111111 | CXCI |
| 11000000 | CXCII |
| 11000001 | CXCIII |
| 11000010 | CXCIV |
| 11000011 | CXCV |
| 11000100 | CXCVI |
| 11000101 | CXCVII |
| 11000110 | CXCVIII |
| 11000111 | CXCIX |
| 11001000 | CC |
| 11001001 | CCI |
| 11001010 | CCII |
| 11001011 | CCIII |
| 11001100 | CCIV |
| 11001101 | CCV |
| 11001110 | CCVI |
| 11001111 | CCVII |
| 11010000 | CCVIII |
| 11010001 | CCIX |
| 11010010 | CCX |
| 11010011 | CCXI |
| 11010100 | CCXII |
| 11010101 | CCXIII |
| 11010110 | CCXIV |
| 11010111 | CCXV |
| 11011000 | CCXVI |
| 11011001 | CCXVII |
| 11011010 | CCXVIII |
| 11011011 | CCXIX |
| 11011100 | CCXX |
| 11011101 | CCXXI |
| 11011110 | CCXXII |
| 11011111 | CCXXIII |
| 11100000 | CCXXIV |
| 11100001 | CCXXV |
| 11100010 | CCXXVI |
| 11100011 | CCXXVII |
| 11100100 | CCXXVIII |
| 11100101 | CCXXIX |
| 11100110 | CCXXX |
| 11100111 | CCXXXI |
| 11101000 | CCXXXII |
| 11101001 | CCXXXIII |
| 11101010 | CCXXXIV |
| 11101011 | CCXXXV |
| 11101100 | CCXXXVI |
| 11101101 | CCXXXVII |
| 11101110 | CCXXXVIII |
| 11101111 | CCXXXIX |
| 11110000 | CCXL |
| 11110001 | CCXLI |
| 11110010 | CCXLII |
| 11110011 | CCXLIII |
| 11110100 | CCXLIV |
| 11110101 | CCXLV |
| 11110110 | CCXLVI |
| 11110111 | CCXLVII |
| 11111000 | CCXLVIII |
| 11111001 | CCXLIX |
| 11111010 | CCL |
| 11111011 | CCLI |
| 11111100 | CCLII |
| 11111101 | CCLIII |
| 11111110 | CCLIV |
| 11111111 | CCLV |
| 100000000 | CCLVI |
| 100000001 | CCLVII |
| 100000010 | CCLVIII |
| 100000011 | CCLIX |
| 100000100 | CCLX |
| 100000101 | CCLXI |
| 100000110 | CCLXII |
| 100000111 | CCLXIII |
| 100001000 | CCLXIV |
| 100001001 | CCLXV |
| 100001010 | CCLXVI |
| 100001011 | CCLXVII |
| 100001100 | CCLXVIII |
| 100001101 | CCLXIX |
| 100001110 | CCLXX |
| 100001111 | CCLXXI |
| 100010000 | CCLXXII |
| 100010001 | CCLXXIII |
| 100010010 | CCLXXIV |
| 100010011 | CCLXXV |
| 100010100 | CCLXXVI |
| 100010101 | CCLXXVII |
| 100010110 | CCLXXVIII |
| 100010111 | CCLXXIX |
| 100011000 | CCLXXX |
| 100011001 | CCLXXXI |
| 100011010 | CCLXXXII |
| 100011011 | CCLXXXIII |
| 100011100 | CCLXXXIV |
| 100011101 | CCLXXXV |
| 100011110 | CCLXXXVI |
| 100011111 | CCLXXXVII |
| 100100000 | CCLXXXVIII |
| 100100001 | CCLXXXIX |
| 100100010 | CCXC |
| 100100011 | CCXCI |
| 100100100 | CCXCII |
| 100100101 | CCXCIII |
| 100100110 | CCXCIV |
| 100100111 | CCXCV |
| 100101000 | CCXCVI |
| 100101001 | CCXCVII |
| 100101010 | CCXCVIII |
| 100101011 | CCXCIX |
| 100101100 | CCC |