Convertir desde Binario (Base 2) a Octal (Base 8)
Realiza la conversión de números entre los distintos sistemas numéricos.
Binario (Base 2) = Octal (Base 8)
Información sobre las unidades de conversión:
Acerca de Binario (Base 2)
El sistema binario es una técnica de numeración donde solo se utilizan dos dígitos, el 0 y el 1. Suele emplearse particularmente en la informática. Es decir, este método se vale solo de dos símbolos, la unidad y el cero. Cualquier número puede expresarse tanto en el sistema decimal como en el binario.
Acerca de Octal (Base 8)
El sistema octal es el sistema de numeración posicional cuya base es 8, utilizando los dígitos indio arábigos: 0,1,2,3,4,5,6,7. En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los dígitos.
Binario (Base 2) vs Octal (Base 8)
| Binario (Base 2) | Octal (Base 8) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
¿Cómo se convierte de Binario (Base 2) a Octal (Base 8)?
Nota: Para convertir un número en binario (base 2) a cualquier otra base, primero debemos convertir el valor binario a base decimal (base 10), para ello debemos realizar los siguientes pasos:
- Identifique cada dígito del número binario.
- Calcule la posición de cada dígito. Empiece desde el dígito más a la derecha, que tendrá una posición de 0. Cada dígito a la izquierda tendrá una posición incremental de 1 (1, 2, 3, etc.).
- Calcule el valor decimal de cada dígito multiplicándolo por la base (2) elevada a la posición del dígito. Por ejemplo: dígito * 2^posición.
- Sume los valores obtenidos en el paso anterior para obtener el número decimal equivalente.
Aplicando estos pasos al número 10011111 binario:
Vamos a ver como pasar el numero binario 10011111 a decimal.
- 1, 0, 0, 1, 1, 1, 1 y 1 son los dígitos.
- Desde el más a la derecha, la posición es 0, 1, 2, 3, 4, 5, 6 y 7.
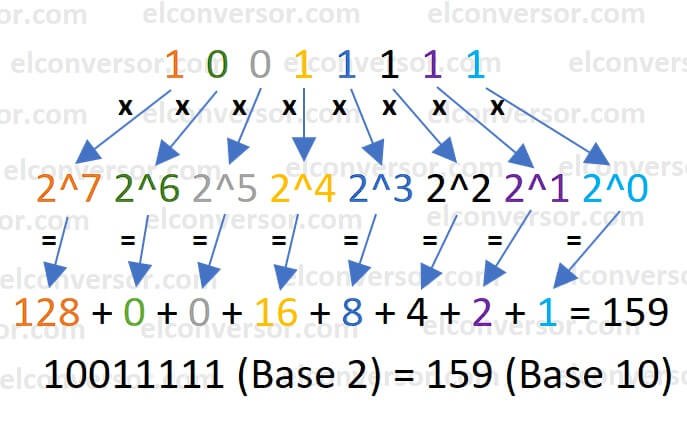
- 1 * 2^7 = 128; 0 * 2^6 = 0; 0 * 2^5 = 0; 1 * 2^4 = 16; 1 * 2^3 = 8; 1 * 2^2 = 4; 1 * 2^1 = 2; 1 * 2^0 = 1;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 decimal.
Entonces, 10011111 binario = 159 decimal.
Nota: Para convertir un número decimal (base 10) a numero octal (base 8), debemos realizar los siguientes pasos:
- Dividir el número decimal entre 8 y anotar los restos de las divisiones hasta que el resultado de la división sea 0.
- Los restos de las divisiones deben ser escritos en orden inverso al que fueron obtenidos, ya que representan los pesos de los dígitos octales correspondientes.
A continuación, se muestra un ejemplo de cómo convertir el número 159 de base decimal a base octal:
- Dividir 159 entre 8: 159 ÷ 8 = 19 con un resto de 7.
- Dividir 19 entre 8: 19 ÷ 8 = 2 con un resto de 3.
- Dividir 2 entre 8: 2 ÷ 8 = 0 con un resto de 2.
Los restos de las divisiones son escritos en orden inverso: 237.
Por lo tanto, el número 159 en base decimal se convierte en 237 en base octal.

Tabla de conversión de Binario (Base 2) a Octal (Base 8)
| Binario (Base 2) | Octal (Base 8) |
|---|---|
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 10 |
| 1001 | 11 |
| 1010 | 12 |
| 1011 | 13 |
| 1100 | 14 |
| 1101 | 15 |
| 1110 | 16 |
| 1111 | 17 |
| 10000 | 20 |
| 10001 | 21 |
| 10010 | 22 |
| 10011 | 23 |
| 10100 | 24 |
| 10101 | 25 |
| 10110 | 26 |
| 10111 | 27 |
| 11000 | 30 |
| 11001 | 31 |
| 11010 | 32 |
| 11011 | 33 |
| 11100 | 34 |
| 11101 | 35 |
| 11110 | 36 |
| 11111 | 37 |
| 100000 | 40 |
| 100001 | 41 |
| 100010 | 42 |
| 100011 | 43 |
| 100100 | 44 |
| 100101 | 45 |
| 100110 | 46 |
| 100111 | 47 |
| 101000 | 50 |
| 101001 | 51 |
| 101010 | 52 |
| 101011 | 53 |
| 101100 | 54 |
| 101101 | 55 |
| 101110 | 56 |
| 101111 | 57 |
| 110000 | 60 |
| 110001 | 61 |
| 110010 | 62 |
| 110011 | 63 |
| 110100 | 64 |
| 110101 | 65 |
| 110110 | 66 |
| 110111 | 67 |
| 111000 | 70 |
| 111001 | 71 |
| 111010 | 72 |
| 111011 | 73 |
| 111100 | 74 |
| 111101 | 75 |
| 111110 | 76 |
| 111111 | 77 |
| 1000000 | 100 |
| 1000001 | 101 |
| 1000010 | 102 |
| 1000011 | 103 |
| 1000100 | 104 |
| 1000101 | 105 |
| 1000110 | 106 |
| 1000111 | 107 |
| 1001000 | 110 |
| 1001001 | 111 |
| 1001010 | 112 |
| 1001011 | 113 |
| 1001100 | 114 |
| 1001101 | 115 |
| 1001110 | 116 |
| 1001111 | 117 |
| 1010000 | 120 |
| 1010001 | 121 |
| 1010010 | 122 |
| 1010011 | 123 |
| 1010100 | 124 |
| 1010101 | 125 |
| 1010110 | 126 |
| 1010111 | 127 |
| 1011000 | 130 |
| 1011001 | 131 |
| 1011010 | 132 |
| 1011011 | 133 |
| 1011100 | 134 |
| 1011101 | 135 |
| 1011110 | 136 |
| 1011111 | 137 |
| 1100000 | 140 |
| 1100001 | 141 |
| 1100010 | 142 |
| 1100011 | 143 |
| 1100100 | 144 |
| 1100101 | 145 |
| 1100110 | 146 |
| 1100111 | 147 |
| 1101000 | 150 |
| 1101001 | 151 |
| 1101010 | 152 |
| 1101011 | 153 |
| 1101100 | 154 |
| 1101101 | 155 |
| 1101110 | 156 |
| 1101111 | 157 |
| 1110000 | 160 |
| 1110001 | 161 |
| 1110010 | 162 |
| 1110011 | 163 |
| 1110100 | 164 |
| 1110101 | 165 |
| 1110110 | 166 |
| 1110111 | 167 |
| 1111000 | 170 |
| 1111001 | 171 |
| 1111010 | 172 |
| 1111011 | 173 |
| 1111100 | 174 |
| 1111101 | 175 |
| 1111110 | 176 |
| 1111111 | 177 |
| 10000000 | 200 |
| 10000001 | 201 |
| 10000010 | 202 |
| 10000011 | 203 |
| 10000100 | 204 |
| 10000101 | 205 |
| 10000110 | 206 |
| 10000111 | 207 |
| 10001000 | 210 |
| 10001001 | 211 |
| 10001010 | 212 |
| 10001011 | 213 |
| 10001100 | 214 |
| 10001101 | 215 |
| 10001110 | 216 |
| 10001111 | 217 |
| 10010000 | 220 |
| 10010001 | 221 |
| 10010010 | 222 |
| 10010011 | 223 |
| 10010100 | 224 |
| 10010101 | 225 |
| 10010110 | 226 |
| 10010111 | 227 |
| 10011000 | 230 |
| 10011001 | 231 |
| 10011010 | 232 |
| 10011011 | 233 |
| 10011100 | 234 |
| 10011101 | 235 |
| 10011110 | 236 |
| 10011111 | 237 |
| 10100000 | 240 |
| 10100001 | 241 |
| 10100010 | 242 |
| 10100011 | 243 |
| 10100100 | 244 |
| 10100101 | 245 |
| 10100110 | 246 |
| 10100111 | 247 |
| 10101000 | 250 |
| 10101001 | 251 |
| 10101010 | 252 |
| 10101011 | 253 |
| 10101100 | 254 |
| 10101101 | 255 |
| 10101110 | 256 |
| 10101111 | 257 |
| 10110000 | 260 |
| 10110001 | 261 |
| 10110010 | 262 |
| 10110011 | 263 |
| 10110100 | 264 |
| 10110101 | 265 |
| 10110110 | 266 |
| 10110111 | 267 |
| 10111000 | 270 |
| 10111001 | 271 |
| 10111010 | 272 |
| 10111011 | 273 |
| 10111100 | 274 |
| 10111101 | 275 |
| 10111110 | 276 |
| 10111111 | 277 |
| 11000000 | 300 |
| 11000001 | 301 |
| 11000010 | 302 |
| 11000011 | 303 |
| 11000100 | 304 |
| 11000101 | 305 |
| 11000110 | 306 |
| 11000111 | 307 |
| 11001000 | 310 |
| 11001001 | 311 |
| 11001010 | 312 |
| 11001011 | 313 |
| 11001100 | 314 |
| 11001101 | 315 |
| 11001110 | 316 |
| 11001111 | 317 |
| 11010000 | 320 |
| 11010001 | 321 |
| 11010010 | 322 |
| 11010011 | 323 |
| 11010100 | 324 |
| 11010101 | 325 |
| 11010110 | 326 |
| 11010111 | 327 |
| 11011000 | 330 |
| 11011001 | 331 |
| 11011010 | 332 |
| 11011011 | 333 |
| 11011100 | 334 |
| 11011101 | 335 |
| 11011110 | 336 |
| 11011111 | 337 |
| 11100000 | 340 |
| 11100001 | 341 |
| 11100010 | 342 |
| 11100011 | 343 |
| 11100100 | 344 |
| 11100101 | 345 |
| 11100110 | 346 |
| 11100111 | 347 |
| 11101000 | 350 |
| 11101001 | 351 |
| 11101010 | 352 |
| 11101011 | 353 |
| 11101100 | 354 |
| 11101101 | 355 |
| 11101110 | 356 |
| 11101111 | 357 |
| 11110000 | 360 |
| 11110001 | 361 |
| 11110010 | 362 |
| 11110011 | 363 |
| 11110100 | 364 |
| 11110101 | 365 |
| 11110110 | 366 |
| 11110111 | 367 |
| 11111000 | 370 |
| 11111001 | 371 |
| 11111010 | 372 |
| 11111011 | 373 |
| 11111100 | 374 |
| 11111101 | 375 |
| 11111110 | 376 |
| 11111111 | 377 |
| 100000000 | 400 |
| 100000001 | 401 |
| 100000010 | 402 |
| 100000011 | 403 |
| 100000100 | 404 |
| 100000101 | 405 |
| 100000110 | 406 |
| 100000111 | 407 |
| 100001000 | 410 |
| 100001001 | 411 |
| 100001010 | 412 |
| 100001011 | 413 |
| 100001100 | 414 |
| 100001101 | 415 |
| 100001110 | 416 |
| 100001111 | 417 |
| 100010000 | 420 |
| 100010001 | 421 |
| 100010010 | 422 |
| 100010011 | 423 |
| 100010100 | 424 |
| 100010101 | 425 |
| 100010110 | 426 |
| 100010111 | 427 |
| 100011000 | 430 |
| 100011001 | 431 |
| 100011010 | 432 |
| 100011011 | 433 |
| 100011100 | 434 |
| 100011101 | 435 |
| 100011110 | 436 |
| 100011111 | 437 |
| 100100000 | 440 |
| 100100001 | 441 |
| 100100010 | 442 |
| 100100011 | 443 |
| 100100100 | 444 |
| 100100101 | 445 |
| 100100110 | 446 |
| 100100111 | 447 |
| 100101000 | 450 |
| 100101001 | 451 |
| 100101010 | 452 |
| 100101011 | 453 |
| 100101100 | 454 |