Converter de Binário (Base 2) para Octal (Base 8)
Realize a conversão de números entre diferentes sistemas numéricos.
Binário (Base 2) = Octal (Base 8)
Informações sobre as unidades de conversão:
Sobre Binário (Base 2)
O sistema binário é uma técnica de numeração que utiliza apenas dois dígitos, 0 e 1. É comumente usado em computação. Este método se baseia exclusivamente em dois símbolos, o um e o zero. Qualquer número pode ser expresso tanto no sistema decimal quanto no binário.
Sobre Octal (Base 8)
O sistema octal é um sistema de numeração posicional com base 8, que utiliza os dígitos arábicos indianos: 0,1,2,3,4,5,6,7. Em informática, às vezes, a numeração octal é utilizada em vez da hexadecimal. Tem a vantagem de não exigir o uso de símbolos diferentes dos dígitos.
Binário (Base 2) vs Octal (Base 8)
| Binário (Base 2) | Octal (Base 8) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
¿Como converter de Binário (Base 2) para Octal (Base 8)?
Nota: Para converter um número em binário (base 2) para qualquer outra base, é necessário primeiro converter o valor binário para decimal (base 10). Siga estes passos:
- Identifique cada dígito do número binário.
- Calcule a posição de cada dígito. Comece pelo dígito mais à direita, que terá uma posição de 0. Cada dígito à esquerda terá uma posição incremental de 1 (1, 2, 3, etc.).
- Calcule o valor decimal de cada dígito multiplicando-o pela base (2) elevada à posição do dígito. Por exemplo: dígito * 2^posição.
- Some os valores obtidos no passo anterior para obter o número decimal equivalente.
Aplicando esses passos ao número binário 10011111:
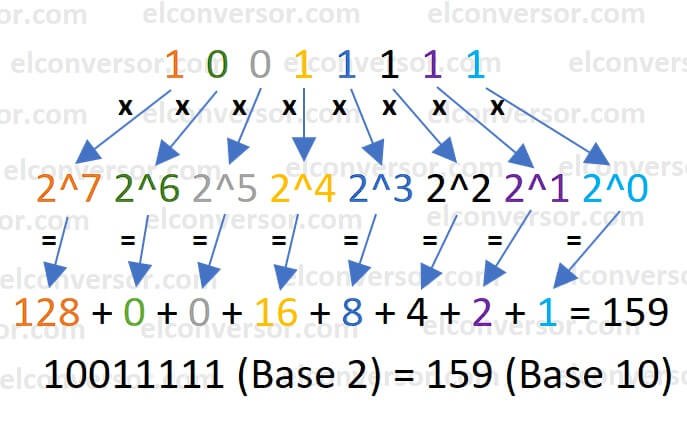
Vamos ver como converter o número binário 10011111 para decimal.
- 1, 0, 0, 1, 1, 1, 1 e 1 são os dígitos.
- Começando pelo mais à direita, as posições são 0, 1, 2, 3, 4, 5, 6 e 7.
- 1 * 2^7 = 128; 0 * 2^6 = 0; 0 * 2^5 = 0; 1 * 2^4 = 16; 1 * 2^3 = 8; 1 * 2^2 = 4; 1 * 2^1 = 2; 1 * 2^0 = 1;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 decimal.
Portanto, 10011111 binário = 159 decimal.
Nota: Para converter um número decimal (base 10) em número octal (base 8), siga os seguintes passos:
- Divida o número decimal por 8 e anote os restos das divisões até que o resultado da divisão seja 0.
- Os restos das divisões devem ser escritos em ordem inversa à obtida, pois representam os pesos dos dígitos octais correspondentes.
Aqui está um exemplo de como converter o número 159 de base decimal para base octal:
- Divida 159 por 8: 159 ÷ 8 = 19 com um resto de 7.
- Divida 19 por 8: 19 ÷ 8 = 2 com um resto de 3.
- Divida 2 por 8: 2 ÷ 8 = 0 com um resto de 2.
Os restos das divisões são escritos em ordem inversa: 237.
Portanto, o número 159 em base decimal é convertido para 237 em base octal.

Tabela de conversão de Binário (Base 2) para Octal (Base 8)
| Binário (Base 2) | Octal (Base 8) |
|---|---|
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 10 |
| 1001 | 11 |
| 1010 | 12 |
| 1011 | 13 |
| 1100 | 14 |
| 1101 | 15 |
| 1110 | 16 |
| 1111 | 17 |
| 10000 | 20 |
| 10001 | 21 |
| 10010 | 22 |
| 10011 | 23 |
| 10100 | 24 |
| 10101 | 25 |
| 10110 | 26 |
| 10111 | 27 |
| 11000 | 30 |
| 11001 | 31 |
| 11010 | 32 |
| 11011 | 33 |
| 11100 | 34 |
| 11101 | 35 |
| 11110 | 36 |
| 11111 | 37 |
| 100000 | 40 |
| 100001 | 41 |
| 100010 | 42 |
| 100011 | 43 |
| 100100 | 44 |
| 100101 | 45 |
| 100110 | 46 |
| 100111 | 47 |
| 101000 | 50 |
| 101001 | 51 |
| 101010 | 52 |
| 101011 | 53 |
| 101100 | 54 |
| 101101 | 55 |
| 101110 | 56 |
| 101111 | 57 |
| 110000 | 60 |
| 110001 | 61 |
| 110010 | 62 |
| 110011 | 63 |
| 110100 | 64 |
| 110101 | 65 |
| 110110 | 66 |
| 110111 | 67 |
| 111000 | 70 |
| 111001 | 71 |
| 111010 | 72 |
| 111011 | 73 |
| 111100 | 74 |
| 111101 | 75 |
| 111110 | 76 |
| 111111 | 77 |
| 1000000 | 100 |
| 1000001 | 101 |
| 1000010 | 102 |
| 1000011 | 103 |
| 1000100 | 104 |
| 1000101 | 105 |
| 1000110 | 106 |
| 1000111 | 107 |
| 1001000 | 110 |
| 1001001 | 111 |
| 1001010 | 112 |
| 1001011 | 113 |
| 1001100 | 114 |
| 1001101 | 115 |
| 1001110 | 116 |
| 1001111 | 117 |
| 1010000 | 120 |
| 1010001 | 121 |
| 1010010 | 122 |
| 1010011 | 123 |
| 1010100 | 124 |
| 1010101 | 125 |
| 1010110 | 126 |
| 1010111 | 127 |
| 1011000 | 130 |
| 1011001 | 131 |
| 1011010 | 132 |
| 1011011 | 133 |
| 1011100 | 134 |
| 1011101 | 135 |
| 1011110 | 136 |
| 1011111 | 137 |
| 1100000 | 140 |
| 1100001 | 141 |
| 1100010 | 142 |
| 1100011 | 143 |
| 1100100 | 144 |
| 1100101 | 145 |
| 1100110 | 146 |
| 1100111 | 147 |
| 1101000 | 150 |
| 1101001 | 151 |
| 1101010 | 152 |
| 1101011 | 153 |
| 1101100 | 154 |
| 1101101 | 155 |
| 1101110 | 156 |
| 1101111 | 157 |
| 1110000 | 160 |
| 1110001 | 161 |
| 1110010 | 162 |
| 1110011 | 163 |
| 1110100 | 164 |
| 1110101 | 165 |
| 1110110 | 166 |
| 1110111 | 167 |
| 1111000 | 170 |
| 1111001 | 171 |
| 1111010 | 172 |
| 1111011 | 173 |
| 1111100 | 174 |
| 1111101 | 175 |
| 1111110 | 176 |
| 1111111 | 177 |
| 10000000 | 200 |
| 10000001 | 201 |
| 10000010 | 202 |
| 10000011 | 203 |
| 10000100 | 204 |
| 10000101 | 205 |
| 10000110 | 206 |
| 10000111 | 207 |
| 10001000 | 210 |
| 10001001 | 211 |
| 10001010 | 212 |
| 10001011 | 213 |
| 10001100 | 214 |
| 10001101 | 215 |
| 10001110 | 216 |
| 10001111 | 217 |
| 10010000 | 220 |
| 10010001 | 221 |
| 10010010 | 222 |
| 10010011 | 223 |
| 10010100 | 224 |
| 10010101 | 225 |
| 10010110 | 226 |
| 10010111 | 227 |
| 10011000 | 230 |
| 10011001 | 231 |
| 10011010 | 232 |
| 10011011 | 233 |
| 10011100 | 234 |
| 10011101 | 235 |
| 10011110 | 236 |
| 10011111 | 237 |
| 10100000 | 240 |
| 10100001 | 241 |
| 10100010 | 242 |
| 10100011 | 243 |
| 10100100 | 244 |
| 10100101 | 245 |
| 10100110 | 246 |
| 10100111 | 247 |
| 10101000 | 250 |
| 10101001 | 251 |
| 10101010 | 252 |
| 10101011 | 253 |
| 10101100 | 254 |
| 10101101 | 255 |
| 10101110 | 256 |
| 10101111 | 257 |
| 10110000 | 260 |
| 10110001 | 261 |
| 10110010 | 262 |
| 10110011 | 263 |
| 10110100 | 264 |
| 10110101 | 265 |
| 10110110 | 266 |
| 10110111 | 267 |
| 10111000 | 270 |
| 10111001 | 271 |
| 10111010 | 272 |
| 10111011 | 273 |
| 10111100 | 274 |
| 10111101 | 275 |
| 10111110 | 276 |
| 10111111 | 277 |
| 11000000 | 300 |
| 11000001 | 301 |
| 11000010 | 302 |
| 11000011 | 303 |
| 11000100 | 304 |
| 11000101 | 305 |
| 11000110 | 306 |
| 11000111 | 307 |
| 11001000 | 310 |
| 11001001 | 311 |
| 11001010 | 312 |
| 11001011 | 313 |
| 11001100 | 314 |
| 11001101 | 315 |
| 11001110 | 316 |
| 11001111 | 317 |
| 11010000 | 320 |
| 11010001 | 321 |
| 11010010 | 322 |
| 11010011 | 323 |
| 11010100 | 324 |
| 11010101 | 325 |
| 11010110 | 326 |
| 11010111 | 327 |
| 11011000 | 330 |
| 11011001 | 331 |
| 11011010 | 332 |
| 11011011 | 333 |
| 11011100 | 334 |
| 11011101 | 335 |
| 11011110 | 336 |
| 11011111 | 337 |
| 11100000 | 340 |
| 11100001 | 341 |
| 11100010 | 342 |
| 11100011 | 343 |
| 11100100 | 344 |
| 11100101 | 345 |
| 11100110 | 346 |
| 11100111 | 347 |
| 11101000 | 350 |
| 11101001 | 351 |
| 11101010 | 352 |
| 11101011 | 353 |
| 11101100 | 354 |
| 11101101 | 355 |
| 11101110 | 356 |
| 11101111 | 357 |
| 11110000 | 360 |
| 11110001 | 361 |
| 11110010 | 362 |
| 11110011 | 363 |
| 11110100 | 364 |
| 11110101 | 365 |
| 11110110 | 366 |
| 11110111 | 367 |
| 11111000 | 370 |
| 11111001 | 371 |
| 11111010 | 372 |
| 11111011 | 373 |
| 11111100 | 374 |
| 11111101 | 375 |
| 11111110 | 376 |
| 11111111 | 377 |
| 100000000 | 400 |
| 100000001 | 401 |
| 100000010 | 402 |
| 100000011 | 403 |
| 100000100 | 404 |
| 100000101 | 405 |
| 100000110 | 406 |
| 100000111 | 407 |
| 100001000 | 410 |
| 100001001 | 411 |
| 100001010 | 412 |
| 100001011 | 413 |
| 100001100 | 414 |
| 100001101 | 415 |
| 100001110 | 416 |
| 100001111 | 417 |
| 100010000 | 420 |
| 100010001 | 421 |
| 100010010 | 422 |
| 100010011 | 423 |
| 100010100 | 424 |
| 100010101 | 425 |
| 100010110 | 426 |
| 100010111 | 427 |
| 100011000 | 430 |
| 100011001 | 431 |
| 100011010 | 432 |
| 100011011 | 433 |
| 100011100 | 434 |
| 100011101 | 435 |
| 100011110 | 436 |
| 100011111 | 437 |
| 100100000 | 440 |
| 100100001 | 441 |
| 100100010 | 442 |
| 100100011 | 443 |
| 100100100 | 444 |
| 100100101 | 445 |
| 100100110 | 446 |
| 100100111 | 447 |
| 100101000 | 450 |
| 100101001 | 451 |
| 100101010 | 452 |
| 100101011 | 453 |
| 100101100 | 454 |