Converti da Romano (Rom) a Binario (Base 2)
Effettua la conversione di numeri tra i diversi sistemi numerici.
Romano (Rom) = Binario (Base 2)
Informazioni sulle unità di conversione:
Informazioni Romano (Rom)
Il sistema di numerazione romano è un antico sistema numerico utilizzato nell'Impero Romano. In questo sistema, le lettere vengono utilizzate per rappresentare i numeri, le lettere più comunemente utilizzate sono I, V, X, L, C, D e M. Ogni lettera ha un valore numerico specifico e vengono combinate in determinati modi per formare i numeri. A differenza del sistema decimale, il sistema di numerazione romano non ha una rappresentazione nativa dello zero. Questo significa che non esiste un simbolo specifico per lo zero nel sistema di numerazione romano. Nonostante ciò, il sistema di numerazione romano è ancora utilizzato in alcuni contesti, come la numerazione degli anni in alcuni calendari.
Informazioni Binario (Base 2)
Il sistema binario è una tecnica di numerazione che utilizza solo due cifre, 0 e 1. È comunemente utilizzato nell'informatica. Questo metodo si basa esclusivamente su due simboli, l'uno e lo zero. Qualsiasi numero può essere espresso sia nel sistema decimale che in quello binario.
Romano (Rom) vs Binario (Base 2)
| Romano (Rom) | Decimal (Base 10) | Binario (Base 2) |
|---|---|---|
| I | 1 | 1 |
| IV | 4 | 100 |
| V | 5 | 101 |
| IX | 9 | 1001 |
| X | 10 | 1010 |
| XL | 40 | 101000 |
| L | 50 | 110010 |
| XC | 90 | 1011010 |
| C | 100 | 1100100 |
| CD | 400 | 110010000 |
| D | 500 | 111110100 |
| CM | 900 | 1110000100 |
| M | 1000 | 1111101000 |
| IV | 4000 | 111110100000 |
| V | 5000 | 1001110001000 |
| IX | 9000 | 10001100101000 |
| X | 10000 | 10011100010000 |
| XL | 40000 | 1001110001000000 |
| L | 50000 | 1100001101010000 |
| XC | 90000 | 10101111110010000 |
| C | 100000 | 11000011010100000 |
| CD | 400000 | 1100001101010000000 |
| D | 500000 | 1111010000100100000 |
| CM | 900000 | 11011011101110100000 |
| M | 1000000 | 11110100001001000000 |
¿Come si converte da Romano (Rom) a Binario (Base 2)?
Nota: Per convertire un numero nel sistema di numerazione romano in qualsiasi altra base, è necessario prima convertire il numero romano in decimale (base 10). Seguire questi passaggi:
Numeri romani e le loro regole di base.
- I numeri romani I, X, C e M possono essere ripetuti fino a tre volte quando si scrive un numero romano composito.
- I numeri romani V, L e D non possono mai essere ripetuti.
- Se un numero romano composito ha un numero più piccolo a destra che a sinistra, allora entrambi vengono sommati. Esempio: XI: Il numero a destra (I = 1) è più piccolo rispetto a sinistra (X = 10), quindi vengono sommati, cioè XI = 11.
- Se un numero romano composito ha un numero più grande a destra ed è I, X o C, allora quello a sinistra viene sottratto da quello a destra. Esempio: IX: Il numero a destra (X = 10) è più grande rispetto a sinistra (I = 1), ed è I, quindi quello a sinistra viene sottratto da quello a destra, cioè IX = 9.
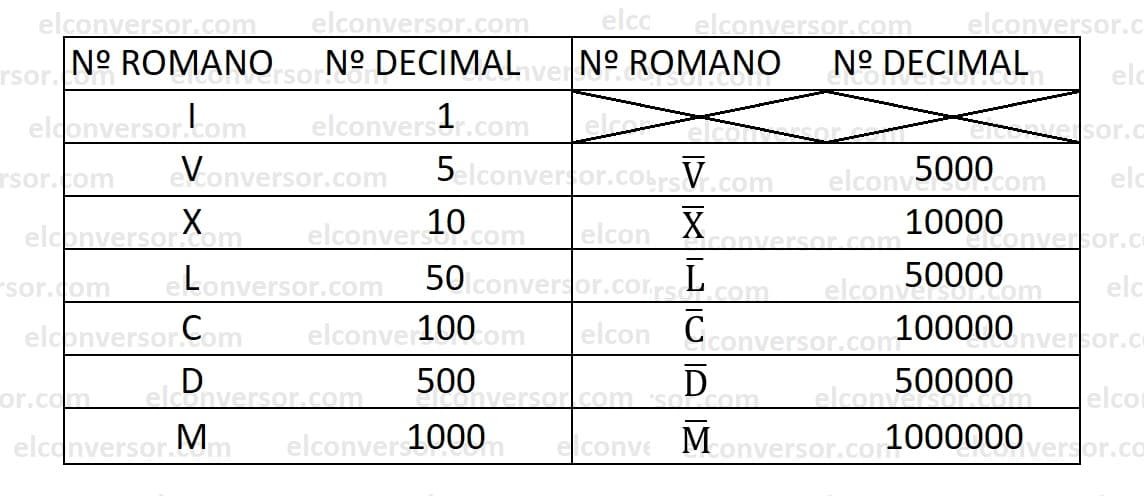
- Se un numero romano ha una linea sopra di esso, il suo valore viene moltiplicato per mille. Esempio: IX
: il numero è 9.000, poiché è il numero romano che rappresenta il 9 e la linea sopra di esso lo moltiplica per mille.
Applicazione dei passaggi al numero romano "CLIX":
- C = 100, L = 50, I = 1, X = 10
- Osserviamo che I = 1 prima di X = 10, quindi I viene sottratto da X;
- Aggiungi 100 + 50 + (10 - 1) = 159.
Il numero romano "CLIX" è equivalente a 159 in decimale.

Nota: Per convertire un numero decimale (base 10) in numero binario (base 2), seguire questi passaggi:
- Dividere ripetutamente il numero decimale per 2 e annotare i resti delle divisioni.
- Il processo termina quando il risultato della divisione è 0.
- I resti delle divisioni devono essere scritti in ordine inverso poiché rappresentano i pesi delle cifre binarie corrispondenti.
Applicando questi passaggi al numero decimale 159:
Ecco un esempio su come convertire il numero decimale 159 in binario:
- Dividere 159 per 2: 159 ÷ 2 = 79 con un resto di 1.
- Dividere 79 per 2: 79 ÷ 2 = 39 con un resto di 1.
- Dividere 39 per 2: 39 ÷ 2 = 19 con un resto di 1.
- Dividere 19 per 2: 19 ÷ 2 = 9 con un resto di 1.
- Dividere 9 per 2: 9 ÷ 2 = 4 con un resto di 1.
- Dividere 4 per 2: 4 ÷ 2 = 2 con un resto di 0.
- Dividere 2 per 2: 2 ÷ 2 = 1 con un resto di 0.
- Dividere 1 per 2: 1 ÷ 2 = 0 con un resto di 1.
I resti delle divisioni vengono scritti in ordine inverso: 10011111.
Quindi, il numero 159 in decimale diventa 10011111 in binario.
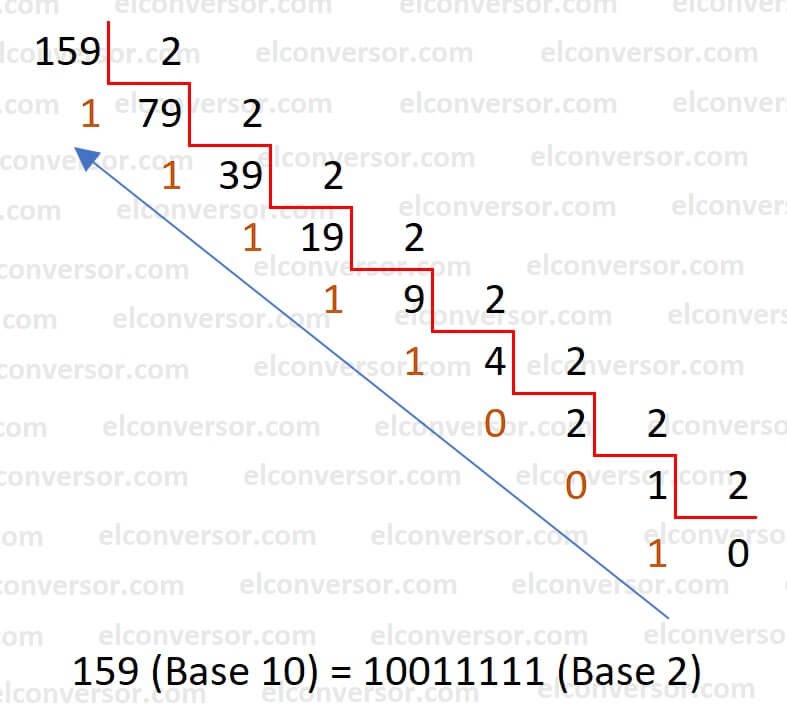
Tabella di conversione di Romano (Rom) a Binario (Base 2)
| Romano (Rom) | Binario (Base 2) |
|---|---|
| I | 1 |
| II | 10 |
| III | 11 |
| IV | 100 |
| V | 101 |
| VI | 110 |
| VII | 111 |
| VIII | 1000 |
| IX | 1001 |
| X | 1010 |
| XI | 1011 |
| XII | 1100 |
| XIII | 1101 |
| XIV | 1110 |
| XV | 1111 |
| XVI | 10000 |
| XVII | 10001 |
| XVIII | 10010 |
| XIX | 10011 |
| XX | 10100 |
| XXI | 10101 |
| XXII | 10110 |
| XXIII | 10111 |
| XXIV | 11000 |
| XXV | 11001 |
| XXVI | 11010 |
| XXVII | 11011 |
| XXVIII | 11100 |
| XXIX | 11101 |
| XXX | 11110 |
| XXXI | 11111 |
| XXXII | 100000 |
| XXXIII | 100001 |
| XXXIV | 100010 |
| XXXV | 100011 |
| XXXVI | 100100 |
| XXXVII | 100101 |
| XXXVIII | 100110 |
| XXXIX | 100111 |
| XL | 101000 |
| XLI | 101001 |
| XLII | 101010 |
| XLIII | 101011 |
| XLIV | 101100 |
| XLV | 101101 |
| XLVI | 101110 |
| XLVII | 101111 |
| XLVIII | 110000 |
| XLIX | 110001 |
| L | 110010 |
| LI | 110011 |
| LII | 110100 |
| LIII | 110101 |
| LIV | 110110 |
| LV | 110111 |
| LVI | 111000 |
| LVII | 111001 |
| LVIII | 111010 |
| LIX | 111011 |
| LX | 111100 |
| LXI | 111101 |
| LXII | 111110 |
| LXIII | 111111 |
| LXIV | 1000000 |
| LXV | 1000001 |
| LXVI | 1000010 |
| LXVII | 1000011 |
| LXVIII | 1000100 |
| LXIX | 1000101 |
| LXX | 1000110 |
| LXXI | 1000111 |
| LXXII | 1001000 |
| LXXIII | 1001001 |
| LXXIV | 1001010 |
| LXXV | 1001011 |
| LXXVI | 1001100 |
| LXXVII | 1001101 |
| LXXVIII | 1001110 |
| LXXIX | 1001111 |
| LXXX | 1010000 |
| LXXXI | 1010001 |
| LXXXII | 1010010 |
| LXXXIII | 1010011 |
| LXXXIV | 1010100 |
| LXXXV | 1010101 |
| LXXXVI | 1010110 |
| LXXXVII | 1010111 |
| LXXXVIII | 1011000 |
| LXXXIX | 1011001 |
| XC | 1011010 |
| XCI | 1011011 |
| XCII | 1011100 |
| XCIII | 1011101 |
| XCIV | 1011110 |
| XCV | 1011111 |
| XCVI | 1100000 |
| XCVII | 1100001 |
| XCVIII | 1100010 |
| XCIX | 1100011 |
| C | 1100100 |
| CI | 1100101 |
| CII | 1100110 |
| CIII | 1100111 |
| CIV | 1101000 |
| CV | 1101001 |
| CVI | 1101010 |
| CVII | 1101011 |
| CVIII | 1101100 |
| CIX | 1101101 |
| CX | 1101110 |
| CXI | 1101111 |
| CXII | 1110000 |
| CXIII | 1110001 |
| CXIV | 1110010 |
| CXV | 1110011 |
| CXVI | 1110100 |
| CXVII | 1110101 |
| CXVIII | 1110110 |
| CXIX | 1110111 |
| CXX | 1111000 |
| CXXI | 1111001 |
| CXXII | 1111010 |
| CXXIII | 1111011 |
| CXXIV | 1111100 |
| CXXV | 1111101 |
| CXXVI | 1111110 |
| CXXVII | 1111111 |
| CXXVIII | 10000000 |
| CXXIX | 10000001 |
| CXXX | 10000010 |
| CXXXI | 10000011 |
| CXXXII | 10000100 |
| CXXXIII | 10000101 |
| CXXXIV | 10000110 |
| CXXXV | 10000111 |
| CXXXVI | 10001000 |
| CXXXVII | 10001001 |
| CXXXVIII | 10001010 |
| CXXXIX | 10001011 |
| CXL | 10001100 |
| CXLI | 10001101 |
| CXLII | 10001110 |
| CXLIII | 10001111 |
| CXLIV | 10010000 |
| CXLV | 10010001 |
| CXLVI | 10010010 |
| CXLVII | 10010011 |
| CXLVIII | 10010100 |
| CXLIX | 10010101 |
| CL | 10010110 |
| CLI | 10010111 |
| CLII | 10011000 |
| CLIII | 10011001 |
| CLIV | 10011010 |
| CLV | 10011011 |
| CLVI | 10011100 |
| CLVII | 10011101 |
| CLVIII | 10011110 |
| CLIX | 10011111 |
| CLX | 10100000 |
| CLXI | 10100001 |
| CLXII | 10100010 |
| CLXIII | 10100011 |
| CLXIV | 10100100 |
| CLXV | 10100101 |
| CLXVI | 10100110 |
| CLXVII | 10100111 |
| CLXVIII | 10101000 |
| CLXIX | 10101001 |
| CLXX | 10101010 |
| CLXXI | 10101011 |
| CLXXII | 10101100 |
| CLXXIII | 10101101 |
| CLXXIV | 10101110 |
| CLXXV | 10101111 |
| CLXXVI | 10110000 |
| CLXXVII | 10110001 |
| CLXXVIII | 10110010 |
| CLXXIX | 10110011 |
| CLXXX | 10110100 |
| CLXXXI | 10110101 |
| CLXXXII | 10110110 |
| CLXXXIII | 10110111 |
| CLXXXIV | 10111000 |
| CLXXXV | 10111001 |
| CLXXXVI | 10111010 |
| CLXXXVII | 10111011 |
| CLXXXVIII | 10111100 |
| CLXXXIX | 10111101 |
| CXC | 10111110 |
| CXCI | 10111111 |
| CXCII | 11000000 |
| CXCIII | 11000001 |
| CXCIV | 11000010 |
| CXCV | 11000011 |
| CXCVI | 11000100 |
| CXCVII | 11000101 |
| CXCVIII | 11000110 |
| CXCIX | 11000111 |
| CC | 11001000 |
| CCI | 11001001 |
| CCII | 11001010 |
| CCIII | 11001011 |
| CCIV | 11001100 |
| CCV | 11001101 |
| CCVI | 11001110 |
| CCVII | 11001111 |
| CCVIII | 11010000 |
| CCIX | 11010001 |
| CCX | 11010010 |
| CCXI | 11010011 |
| CCXII | 11010100 |
| CCXIII | 11010101 |
| CCXIV | 11010110 |
| CCXV | 11010111 |
| CCXVI | 11011000 |
| CCXVII | 11011001 |
| CCXVIII | 11011010 |
| CCXIX | 11011011 |
| CCXX | 11011100 |
| CCXXI | 11011101 |
| CCXXII | 11011110 |
| CCXXIII | 11011111 |
| CCXXIV | 11100000 |
| CCXXV | 11100001 |
| CCXXVI | 11100010 |
| CCXXVII | 11100011 |
| CCXXVIII | 11100100 |
| CCXXIX | 11100101 |
| CCXXX | 11100110 |
| CCXXXI | 11100111 |
| CCXXXII | 11101000 |
| CCXXXIII | 11101001 |
| CCXXXIV | 11101010 |
| CCXXXV | 11101011 |
| CCXXXVI | 11101100 |
| CCXXXVII | 11101101 |
| CCXXXVIII | 11101110 |
| CCXXXIX | 11101111 |
| CCXL | 11110000 |
| CCXLI | 11110001 |
| CCXLII | 11110010 |
| CCXLIII | 11110011 |
| CCXLIV | 11110100 |
| CCXLV | 11110101 |
| CCXLVI | 11110110 |
| CCXLVII | 11110111 |
| CCXLVIII | 11111000 |
| CCXLIX | 11111001 |
| CCL | 11111010 |
| CCLI | 11111011 |
| CCLII | 11111100 |
| CCLIII | 11111101 |
| CCLIV | 11111110 |
| CCLV | 11111111 |
| CCLVI | 100000000 |
| CCLVII | 100000001 |
| CCLVIII | 100000010 |
| CCLIX | 100000011 |
| CCLX | 100000100 |
| CCLXI | 100000101 |
| CCLXII | 100000110 |
| CCLXIII | 100000111 |
| CCLXIV | 100001000 |
| CCLXV | 100001001 |
| CCLXVI | 100001010 |
| CCLXVII | 100001011 |
| CCLXVIII | 100001100 |
| CCLXIX | 100001101 |
| CCLXX | 100001110 |
| CCLXXI | 100001111 |
| CCLXXII | 100010000 |
| CCLXXIII | 100010001 |
| CCLXXIV | 100010010 |
| CCLXXV | 100010011 |
| CCLXXVI | 100010100 |
| CCLXXVII | 100010101 |
| CCLXXVIII | 100010110 |
| CCLXXIX | 100010111 |
| CCLXXX | 100011000 |
| CCLXXXI | 100011001 |
| CCLXXXII | 100011010 |
| CCLXXXIII | 100011011 |
| CCLXXXIV | 100011100 |
| CCLXXXV | 100011101 |
| CCLXXXVI | 100011110 |
| CCLXXXVII | 100011111 |
| CCLXXXVIII | 100100000 |
| CCLXXXIX | 100100001 |
| CCXC | 100100010 |
| CCXCI | 100100011 |
| CCXCII | 100100100 |
| CCXCIII | 100100101 |
| CCXCIV | 100100110 |
| CCXCV | 100100111 |
| CCXCVI | 100101000 |
| CCXCVII | 100101001 |
| CCXCVIII | 100101010 |
| CCXCIX | 100101011 |
| CCC | 100101100 |