Convertir de Romain (Rom) à Binaire (Base 2)
Effectuez la conversion de nombres entre différents systèmes numériques.
Romain (Rom) = Binaire (Base 2)
Informations sur les unités de conversion:
À propos de Romain (Rom)
Le système de numérotation romaine est un ancien système numérique utilisé dans l'Empire romain. Dans ce système, des lettres sont utilisées pour représenter des chiffres, les lettres les plus couramment utilisées étant I, V, X, L, C, D et M. Chaque lettre a une valeur numérique spécifique et elles sont combinées de certaines manières pour former des chiffres. Contrairement au système décimal, le système de numérotation romaine n'a pas de représentation native du zéro. Autrement dit, il n'existe pas de symbole spécifique pour le zéro dans le système de numérotation romaine. Malgré cela, le système de numérotation romaine est toujours utilisé dans certains contextes, tels que la numérotation des années dans certains calendriers.
À propos de Binaire (Base 2)
Le système binaire est une technique de numération qui utilise uniquement deux chiffres, 0 et 1. Il est couramment utilisé en informatique. Cette méthode repose uniquement sur deux symboles, le un et le zéro. Tout nombre peut être exprimé à la fois dans le système décimal et binaire.
Romain (Rom) vs Binaire (Base 2)
| Romain (Rom) | Decimal (Base 10) | Binaire (Base 2) |
|---|---|---|
| I | 1 | 1 |
| IV | 4 | 100 |
| V | 5 | 101 |
| IX | 9 | 1001 |
| X | 10 | 1010 |
| XL | 40 | 101000 |
| L | 50 | 110010 |
| XC | 90 | 1011010 |
| C | 100 | 1100100 |
| CD | 400 | 110010000 |
| D | 500 | 111110100 |
| CM | 900 | 1110000100 |
| M | 1000 | 1111101000 |
| IV | 4000 | 111110100000 |
| V | 5000 | 1001110001000 |
| IX | 9000 | 10001100101000 |
| X | 10000 | 10011100010000 |
| XL | 40000 | 1001110001000000 |
| L | 50000 | 1100001101010000 |
| XC | 90000 | 10101111110010000 |
| C | 100000 | 11000011010100000 |
| CD | 400000 | 1100001101010000000 |
| D | 500000 | 1111010000100100000 |
| CM | 900000 | 11011011101110100000 |
| M | 1000000 | 11110100001001000000 |
¿Comment convertir de Romain (Rom) à Binaire (Base 2)?
Remarque : Pour convertir un nombre dans le système de numérotation romaine en une autre base, nous devons d'abord convertir le nombre en numérotation romaine en décimal (base 10). Suivez ces étapes :
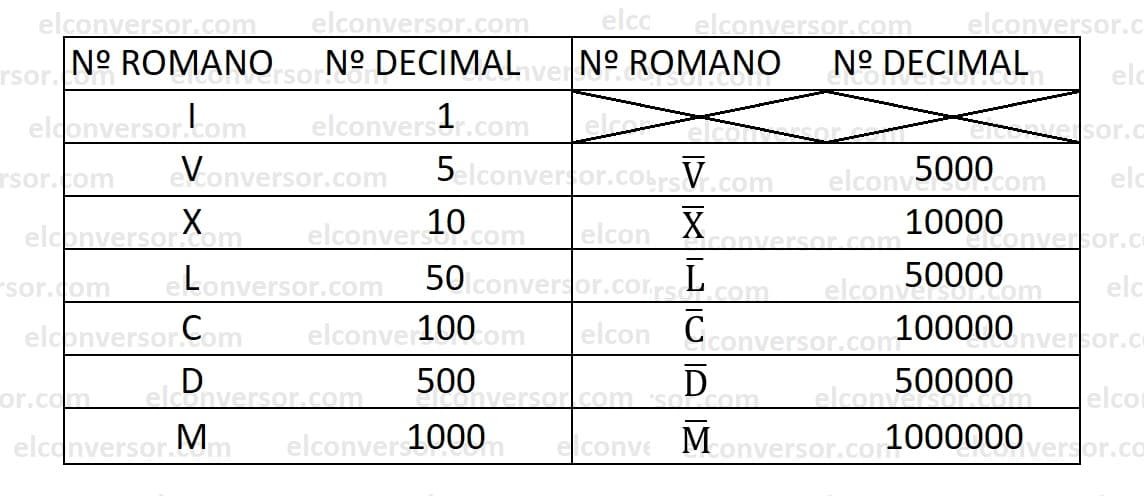
Chiffres romains et leurs règles de base.
- Les chiffres romains I, X, C et M peuvent être répétés jusqu'à trois fois lors de l'écriture d'un chiffre romain composite.
- Les chiffres romains V, L et D ne peuvent jamais être répétés.
- Si un chiffre romain composite a un chiffre plus petit à droite qu'à gauche, les deux sont ajoutés. Exemple : XI : Le chiffre à droite (I = 1) est plus petit qu'à gauche (X = 10), donc ils sont ajoutés, c'est-à-dire XI = 11.
- Si un chiffre romain composite a un chiffre plus grand à droite et qu'il s'agit de I, X ou C, alors le chiffre de gauche est soustrait de celui de droite. Exemple : IX : Le chiffre à droite (X = 10) est plus grand qu'à gauche (I = 1), et c'est I, donc le chiffre de gauche est soustrait de celui de droite, c'est-à-dire IX = 9.
- Si un chiffre romain a une ligne au-dessus, sa valeur est multipliée par mille. Exemple : IX
: le chiffre est 9 000, car c'est le chiffre romain représentant 9 et la ligne au-dessus le multiplie par mille.
Application des étapes au chiffre romain "CLIX" :
- C = 100, L = 50, I = 1, X = 10
- Nous observons que I = 1 avant X = 10, donc I est soustrait de X ;
- Ajoutez 100 + 50 + (10 - 1) = 159.
Le chiffre romain "CLIX" est équivalent à 159 en décimal.

Remarque : Pour convertir un nombre décimal (base 10) en nombre binaire (base 2), suivez ces étapes :
- Divisez le nombre décimal par 2 de manière répétée et notez les restes des divisions.
- Le processus se termine lorsque le résultat de la division est égal à 0.
- Les restes des divisions doivent être écrits dans l'ordre inverse car ils représentent les poids des chiffres binaires correspondants.
Application de ces étapes au nombre décimal 159 :
Voici un exemple de conversion du nombre décimal 159 en binaire :
- Divisez 159 par 2 : 159 ÷ 2 = 79 avec un reste de 1.
- Divisez 79 par 2 : 79 ÷ 2 = 39 avec un reste de 1.
- Divisez 39 par 2 : 39 ÷ 2 = 19 avec un reste de 1.
- Divisez 19 par 2 : 19 ÷ 2 = 9 avec un reste de 1.
- Divisez 9 par 2 : 9 ÷ 2 = 4 avec un reste de 1.
- Divisez 4 par 2 : 4 ÷ 2 = 2 avec un reste de 0.
- Divisez 2 par 2 : 2 ÷ 2 = 1 avec un reste de 0.
- Divisez 1 par 2 : 1 ÷ 2 = 0 avec un reste de 1.
Les restes des divisions sont écrits dans l'ordre inverse : 10011111.
Ainsi, le nombre 159 en décimal se convertit en 10011111 en binaire.
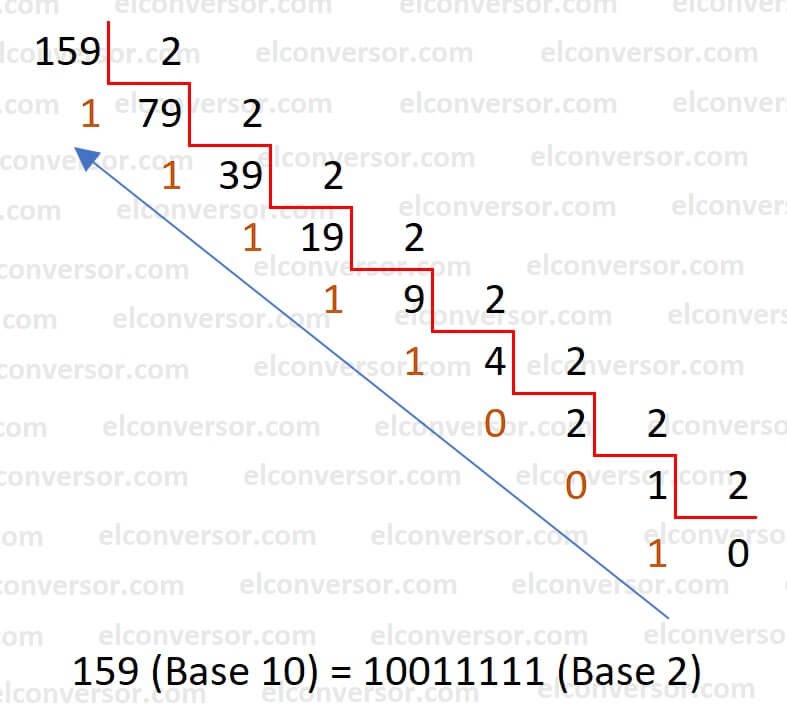
Table de conversion de Romain (Rom) à Binaire (Base 2)
| Romain (Rom) | Binaire (Base 2) |
|---|---|
| I | 1 |
| II | 10 |
| III | 11 |
| IV | 100 |
| V | 101 |
| VI | 110 |
| VII | 111 |
| VIII | 1000 |
| IX | 1001 |
| X | 1010 |
| XI | 1011 |
| XII | 1100 |
| XIII | 1101 |
| XIV | 1110 |
| XV | 1111 |
| XVI | 10000 |
| XVII | 10001 |
| XVIII | 10010 |
| XIX | 10011 |
| XX | 10100 |
| XXI | 10101 |
| XXII | 10110 |
| XXIII | 10111 |
| XXIV | 11000 |
| XXV | 11001 |
| XXVI | 11010 |
| XXVII | 11011 |
| XXVIII | 11100 |
| XXIX | 11101 |
| XXX | 11110 |
| XXXI | 11111 |
| XXXII | 100000 |
| XXXIII | 100001 |
| XXXIV | 100010 |
| XXXV | 100011 |
| XXXVI | 100100 |
| XXXVII | 100101 |
| XXXVIII | 100110 |
| XXXIX | 100111 |
| XL | 101000 |
| XLI | 101001 |
| XLII | 101010 |
| XLIII | 101011 |
| XLIV | 101100 |
| XLV | 101101 |
| XLVI | 101110 |
| XLVII | 101111 |
| XLVIII | 110000 |
| XLIX | 110001 |
| L | 110010 |
| LI | 110011 |
| LII | 110100 |
| LIII | 110101 |
| LIV | 110110 |
| LV | 110111 |
| LVI | 111000 |
| LVII | 111001 |
| LVIII | 111010 |
| LIX | 111011 |
| LX | 111100 |
| LXI | 111101 |
| LXII | 111110 |
| LXIII | 111111 |
| LXIV | 1000000 |
| LXV | 1000001 |
| LXVI | 1000010 |
| LXVII | 1000011 |
| LXVIII | 1000100 |
| LXIX | 1000101 |
| LXX | 1000110 |
| LXXI | 1000111 |
| LXXII | 1001000 |
| LXXIII | 1001001 |
| LXXIV | 1001010 |
| LXXV | 1001011 |
| LXXVI | 1001100 |
| LXXVII | 1001101 |
| LXXVIII | 1001110 |
| LXXIX | 1001111 |
| LXXX | 1010000 |
| LXXXI | 1010001 |
| LXXXII | 1010010 |
| LXXXIII | 1010011 |
| LXXXIV | 1010100 |
| LXXXV | 1010101 |
| LXXXVI | 1010110 |
| LXXXVII | 1010111 |
| LXXXVIII | 1011000 |
| LXXXIX | 1011001 |
| XC | 1011010 |
| XCI | 1011011 |
| XCII | 1011100 |
| XCIII | 1011101 |
| XCIV | 1011110 |
| XCV | 1011111 |
| XCVI | 1100000 |
| XCVII | 1100001 |
| XCVIII | 1100010 |
| XCIX | 1100011 |
| C | 1100100 |
| CI | 1100101 |
| CII | 1100110 |
| CIII | 1100111 |
| CIV | 1101000 |
| CV | 1101001 |
| CVI | 1101010 |
| CVII | 1101011 |
| CVIII | 1101100 |
| CIX | 1101101 |
| CX | 1101110 |
| CXI | 1101111 |
| CXII | 1110000 |
| CXIII | 1110001 |
| CXIV | 1110010 |
| CXV | 1110011 |
| CXVI | 1110100 |
| CXVII | 1110101 |
| CXVIII | 1110110 |
| CXIX | 1110111 |
| CXX | 1111000 |
| CXXI | 1111001 |
| CXXII | 1111010 |
| CXXIII | 1111011 |
| CXXIV | 1111100 |
| CXXV | 1111101 |
| CXXVI | 1111110 |
| CXXVII | 1111111 |
| CXXVIII | 10000000 |
| CXXIX | 10000001 |
| CXXX | 10000010 |
| CXXXI | 10000011 |
| CXXXII | 10000100 |
| CXXXIII | 10000101 |
| CXXXIV | 10000110 |
| CXXXV | 10000111 |
| CXXXVI | 10001000 |
| CXXXVII | 10001001 |
| CXXXVIII | 10001010 |
| CXXXIX | 10001011 |
| CXL | 10001100 |
| CXLI | 10001101 |
| CXLII | 10001110 |
| CXLIII | 10001111 |
| CXLIV | 10010000 |
| CXLV | 10010001 |
| CXLVI | 10010010 |
| CXLVII | 10010011 |
| CXLVIII | 10010100 |
| CXLIX | 10010101 |
| CL | 10010110 |
| CLI | 10010111 |
| CLII | 10011000 |
| CLIII | 10011001 |
| CLIV | 10011010 |
| CLV | 10011011 |
| CLVI | 10011100 |
| CLVII | 10011101 |
| CLVIII | 10011110 |
| CLIX | 10011111 |
| CLX | 10100000 |
| CLXI | 10100001 |
| CLXII | 10100010 |
| CLXIII | 10100011 |
| CLXIV | 10100100 |
| CLXV | 10100101 |
| CLXVI | 10100110 |
| CLXVII | 10100111 |
| CLXVIII | 10101000 |
| CLXIX | 10101001 |
| CLXX | 10101010 |
| CLXXI | 10101011 |
| CLXXII | 10101100 |
| CLXXIII | 10101101 |
| CLXXIV | 10101110 |
| CLXXV | 10101111 |
| CLXXVI | 10110000 |
| CLXXVII | 10110001 |
| CLXXVIII | 10110010 |
| CLXXIX | 10110011 |
| CLXXX | 10110100 |
| CLXXXI | 10110101 |
| CLXXXII | 10110110 |
| CLXXXIII | 10110111 |
| CLXXXIV | 10111000 |
| CLXXXV | 10111001 |
| CLXXXVI | 10111010 |
| CLXXXVII | 10111011 |
| CLXXXVIII | 10111100 |
| CLXXXIX | 10111101 |
| CXC | 10111110 |
| CXCI | 10111111 |
| CXCII | 11000000 |
| CXCIII | 11000001 |
| CXCIV | 11000010 |
| CXCV | 11000011 |
| CXCVI | 11000100 |
| CXCVII | 11000101 |
| CXCVIII | 11000110 |
| CXCIX | 11000111 |
| CC | 11001000 |
| CCI | 11001001 |
| CCII | 11001010 |
| CCIII | 11001011 |
| CCIV | 11001100 |
| CCV | 11001101 |
| CCVI | 11001110 |
| CCVII | 11001111 |
| CCVIII | 11010000 |
| CCIX | 11010001 |
| CCX | 11010010 |
| CCXI | 11010011 |
| CCXII | 11010100 |
| CCXIII | 11010101 |
| CCXIV | 11010110 |
| CCXV | 11010111 |
| CCXVI | 11011000 |
| CCXVII | 11011001 |
| CCXVIII | 11011010 |
| CCXIX | 11011011 |
| CCXX | 11011100 |
| CCXXI | 11011101 |
| CCXXII | 11011110 |
| CCXXIII | 11011111 |
| CCXXIV | 11100000 |
| CCXXV | 11100001 |
| CCXXVI | 11100010 |
| CCXXVII | 11100011 |
| CCXXVIII | 11100100 |
| CCXXIX | 11100101 |
| CCXXX | 11100110 |
| CCXXXI | 11100111 |
| CCXXXII | 11101000 |
| CCXXXIII | 11101001 |
| CCXXXIV | 11101010 |
| CCXXXV | 11101011 |
| CCXXXVI | 11101100 |
| CCXXXVII | 11101101 |
| CCXXXVIII | 11101110 |
| CCXXXIX | 11101111 |
| CCXL | 11110000 |
| CCXLI | 11110001 |
| CCXLII | 11110010 |
| CCXLIII | 11110011 |
| CCXLIV | 11110100 |
| CCXLV | 11110101 |
| CCXLVI | 11110110 |
| CCXLVII | 11110111 |
| CCXLVIII | 11111000 |
| CCXLIX | 11111001 |
| CCL | 11111010 |
| CCLI | 11111011 |
| CCLII | 11111100 |
| CCLIII | 11111101 |
| CCLIV | 11111110 |
| CCLV | 11111111 |
| CCLVI | 100000000 |
| CCLVII | 100000001 |
| CCLVIII | 100000010 |
| CCLIX | 100000011 |
| CCLX | 100000100 |
| CCLXI | 100000101 |
| CCLXII | 100000110 |
| CCLXIII | 100000111 |
| CCLXIV | 100001000 |
| CCLXV | 100001001 |
| CCLXVI | 100001010 |
| CCLXVII | 100001011 |
| CCLXVIII | 100001100 |
| CCLXIX | 100001101 |
| CCLXX | 100001110 |
| CCLXXI | 100001111 |
| CCLXXII | 100010000 |
| CCLXXIII | 100010001 |
| CCLXXIV | 100010010 |
| CCLXXV | 100010011 |
| CCLXXVI | 100010100 |
| CCLXXVII | 100010101 |
| CCLXXVIII | 100010110 |
| CCLXXIX | 100010111 |
| CCLXXX | 100011000 |
| CCLXXXI | 100011001 |
| CCLXXXII | 100011010 |
| CCLXXXIII | 100011011 |
| CCLXXXIV | 100011100 |
| CCLXXXV | 100011101 |
| CCLXXXVI | 100011110 |
| CCLXXXVII | 100011111 |
| CCLXXXVIII | 100100000 |
| CCLXXXIX | 100100001 |
| CCXC | 100100010 |
| CCXCI | 100100011 |
| CCXCII | 100100100 |
| CCXCIII | 100100101 |
| CCXCIV | 100100110 |
| CCXCV | 100100111 |
| CCXCVI | 100101000 |
| CCXCVII | 100101001 |
| CCXCVIII | 100101010 |
| CCXCIX | 100101011 |
| CCC | 100101100 |