Convertir de Octal (Base 8) à Binaire (Base 2)
Effectuez la conversion de nombres entre différents systèmes numériques.
Octal (Base 8) = Binaire (Base 2)
Informations sur les unités de conversion:
À propos de Octal (Base 8)
Le système octal est le système de numération positionnelle avec une base de 8, utilisant les chiffres indo-arabes : 0, 1, 2, 3, 4, 5, 6, 7. En informatique, la numération octale est parfois utilisée à la place de l'hexadécimal. Elle présente l'avantage de ne pas nécessiter d'autres symboles que les chiffres.
À propos de Binaire (Base 2)
Le système binaire est une technique de numération qui utilise uniquement deux chiffres, 0 et 1. Il est couramment utilisé en informatique. Cette méthode repose uniquement sur deux symboles, le un et le zéro. Tout nombre peut être exprimé à la fois dans le système décimal et binaire.
Octal (Base 8) vs Binaire (Base 2)
| Octal (Base 8) | Binaire (Base 2) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
¿Comment convertir de Octal (Base 8) à Binaire (Base 2)?
Note : Pour convertir un nombre de l'octal (base 8) vers n'importe quelle autre base, nous devons d'abord convertir la valeur octale en décimal (base 10). Pour ce faire, suivez ces étapes :
- Identifiez chaque chiffre du nombre octal.
- Calculez la position de chaque chiffre. Commencez par le chiffre le plus à droite, qui aura une position de 0. Chaque chiffre à gauche aura une position incrémentielle de 1 (1, 2, 3, etc.).
- Calculez la valeur décimale de chaque chiffre en le multipliant par la base (8) élevée à la position du chiffre. Par exemple : chiffre * 8^position.
- Additionnez les valeurs obtenues à l'étape précédente pour obtenir le nombre décimal équivalent.
Application de ces étapes au nombre octal 237 :
- 2, 3 et 7 sont les chiffres.
- De droite à gauche, les positions sont 0, 1 et 2.
- 2 * 8^2 = 128 ; 3 * 8^1 = 24 ; 7 * 8^0 = 7.
- 128 + 24 + 7 = 159 décimal
Par conséquent, 237 octal = 159 décimal.

Remarque : Pour convertir un nombre décimal (base 10) en nombre binaire (base 2), suivez ces étapes :
- Divisez le nombre décimal par 2 de manière répétée et notez les restes des divisions.
- Le processus se termine lorsque le résultat de la division est égal à 0.
- Les restes des divisions doivent être écrits dans l'ordre inverse car ils représentent les poids des chiffres binaires correspondants.
Application de ces étapes au nombre décimal 159 :
Voici un exemple de conversion du nombre décimal 159 en binaire :
- Divisez 159 par 2 : 159 ÷ 2 = 79 avec un reste de 1.
- Divisez 79 par 2 : 79 ÷ 2 = 39 avec un reste de 1.
- Divisez 39 par 2 : 39 ÷ 2 = 19 avec un reste de 1.
- Divisez 19 par 2 : 19 ÷ 2 = 9 avec un reste de 1.
- Divisez 9 par 2 : 9 ÷ 2 = 4 avec un reste de 1.
- Divisez 4 par 2 : 4 ÷ 2 = 2 avec un reste de 0.
- Divisez 2 par 2 : 2 ÷ 2 = 1 avec un reste de 0.
- Divisez 1 par 2 : 1 ÷ 2 = 0 avec un reste de 1.
Les restes des divisions sont écrits dans l'ordre inverse : 10011111.
Ainsi, le nombre 159 en décimal se convertit en 10011111 en binaire.
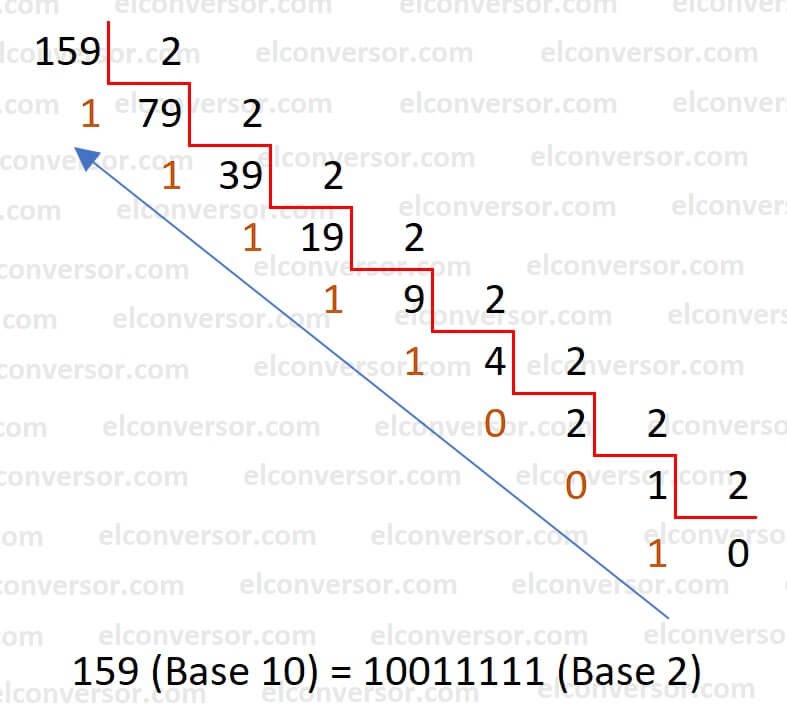
Table de conversion de Octal (Base 8) à Binaire (Base 2)
| Octal (Base 8) | Binaire (Base 2) |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 10 | 1000 |
| 11 | 1001 |
| 12 | 1010 |
| 13 | 1011 |
| 14 | 1100 |
| 15 | 1101 |
| 16 | 1110 |
| 17 | 1111 |
| 20 | 10000 |
| 21 | 10001 |
| 22 | 10010 |
| 23 | 10011 |
| 24 | 10100 |
| 25 | 10101 |
| 26 | 10110 |
| 27 | 10111 |
| 30 | 11000 |
| 31 | 11001 |
| 32 | 11010 |
| 33 | 11011 |
| 34 | 11100 |
| 35 | 11101 |
| 36 | 11110 |
| 37 | 11111 |
| 40 | 100000 |
| 41 | 100001 |
| 42 | 100010 |
| 43 | 100011 |
| 44 | 100100 |
| 45 | 100101 |
| 46 | 100110 |
| 47 | 100111 |
| 50 | 101000 |
| 51 | 101001 |
| 52 | 101010 |
| 53 | 101011 |
| 54 | 101100 |
| 55 | 101101 |
| 56 | 101110 |
| 57 | 101111 |
| 60 | 110000 |
| 61 | 110001 |
| 62 | 110010 |
| 63 | 110011 |
| 64 | 110100 |
| 65 | 110101 |
| 66 | 110110 |
| 67 | 110111 |
| 70 | 111000 |
| 71 | 111001 |
| 72 | 111010 |
| 73 | 111011 |
| 74 | 111100 |
| 75 | 111101 |
| 76 | 111110 |
| 77 | 111111 |
| 100 | 1000000 |
| 101 | 1000001 |
| 102 | 1000010 |
| 103 | 1000011 |
| 104 | 1000100 |
| 105 | 1000101 |
| 106 | 1000110 |
| 107 | 1000111 |
| 110 | 1001000 |
| 111 | 1001001 |
| 112 | 1001010 |
| 113 | 1001011 |
| 114 | 1001100 |
| 115 | 1001101 |
| 116 | 1001110 |
| 117 | 1001111 |
| 120 | 1010000 |
| 121 | 1010001 |
| 122 | 1010010 |
| 123 | 1010011 |
| 124 | 1010100 |
| 125 | 1010101 |
| 126 | 1010110 |
| 127 | 1010111 |
| 130 | 1011000 |
| 131 | 1011001 |
| 132 | 1011010 |
| 133 | 1011011 |
| 134 | 1011100 |
| 135 | 1011101 |
| 136 | 1011110 |
| 137 | 1011111 |
| 140 | 1100000 |
| 141 | 1100001 |
| 142 | 1100010 |
| 143 | 1100011 |
| 144 | 1100100 |
| 145 | 1100101 |
| 146 | 1100110 |
| 147 | 1100111 |
| 150 | 1101000 |
| 151 | 1101001 |
| 152 | 1101010 |
| 153 | 1101011 |
| 154 | 1101100 |
| 155 | 1101101 |
| 156 | 1101110 |
| 157 | 1101111 |
| 160 | 1110000 |
| 161 | 1110001 |
| 162 | 1110010 |
| 163 | 1110011 |
| 164 | 1110100 |
| 165 | 1110101 |
| 166 | 1110110 |
| 167 | 1110111 |
| 170 | 1111000 |
| 171 | 1111001 |
| 172 | 1111010 |
| 173 | 1111011 |
| 174 | 1111100 |
| 175 | 1111101 |
| 176 | 1111110 |
| 177 | 1111111 |
| 200 | 10000000 |
| 201 | 10000001 |
| 202 | 10000010 |
| 203 | 10000011 |
| 204 | 10000100 |
| 205 | 10000101 |
| 206 | 10000110 |
| 207 | 10000111 |
| 210 | 10001000 |
| 211 | 10001001 |
| 212 | 10001010 |
| 213 | 10001011 |
| 214 | 10001100 |
| 215 | 10001101 |
| 216 | 10001110 |
| 217 | 10001111 |
| 220 | 10010000 |
| 221 | 10010001 |
| 222 | 10010010 |
| 223 | 10010011 |
| 224 | 10010100 |
| 225 | 10010101 |
| 226 | 10010110 |
| 227 | 10010111 |
| 230 | 10011000 |
| 231 | 10011001 |
| 232 | 10011010 |
| 233 | 10011011 |
| 234 | 10011100 |
| 235 | 10011101 |
| 236 | 10011110 |
| 237 | 10011111 |
| 240 | 10100000 |
| 241 | 10100001 |
| 242 | 10100010 |
| 243 | 10100011 |
| 244 | 10100100 |
| 245 | 10100101 |
| 246 | 10100110 |
| 247 | 10100111 |
| 250 | 10101000 |
| 251 | 10101001 |
| 252 | 10101010 |
| 253 | 10101011 |
| 254 | 10101100 |
| 255 | 10101101 |
| 256 | 10101110 |
| 257 | 10101111 |
| 260 | 10110000 |
| 261 | 10110001 |
| 262 | 10110010 |
| 263 | 10110011 |
| 264 | 10110100 |
| 265 | 10110101 |
| 266 | 10110110 |
| 267 | 10110111 |
| 270 | 10111000 |
| 271 | 10111001 |
| 272 | 10111010 |
| 273 | 10111011 |
| 274 | 10111100 |
| 275 | 10111101 |
| 276 | 10111110 |
| 277 | 10111111 |
| 300 | 11000000 |
| 301 | 11000001 |
| 302 | 11000010 |
| 303 | 11000011 |
| 304 | 11000100 |
| 305 | 11000101 |
| 306 | 11000110 |
| 307 | 11000111 |
| 310 | 11001000 |
| 311 | 11001001 |
| 312 | 11001010 |
| 313 | 11001011 |
| 314 | 11001100 |
| 315 | 11001101 |
| 316 | 11001110 |
| 317 | 11001111 |
| 320 | 11010000 |
| 321 | 11010001 |
| 322 | 11010010 |
| 323 | 11010011 |
| 324 | 11010100 |
| 325 | 11010101 |
| 326 | 11010110 |
| 327 | 11010111 |
| 330 | 11011000 |
| 331 | 11011001 |
| 332 | 11011010 |
| 333 | 11011011 |
| 334 | 11011100 |
| 335 | 11011101 |
| 336 | 11011110 |
| 337 | 11011111 |
| 340 | 11100000 |
| 341 | 11100001 |
| 342 | 11100010 |
| 343 | 11100011 |
| 344 | 11100100 |
| 345 | 11100101 |
| 346 | 11100110 |
| 347 | 11100111 |
| 350 | 11101000 |
| 351 | 11101001 |
| 352 | 11101010 |
| 353 | 11101011 |
| 354 | 11101100 |
| 355 | 11101101 |
| 356 | 11101110 |
| 357 | 11101111 |
| 360 | 11110000 |
| 361 | 11110001 |
| 362 | 11110010 |
| 363 | 11110011 |
| 364 | 11110100 |
| 365 | 11110101 |
| 366 | 11110110 |
| 367 | 11110111 |
| 370 | 11111000 |
| 371 | 11111001 |
| 372 | 11111010 |
| 373 | 11111011 |
| 374 | 11111100 |
| 375 | 11111101 |
| 376 | 11111110 |
| 377 | 11111111 |
| 400 | 100000000 |
| 401 | 100000001 |
| 402 | 100000010 |
| 403 | 100000011 |
| 404 | 100000100 |
| 405 | 100000101 |
| 406 | 100000110 |
| 407 | 100000111 |
| 410 | 100001000 |
| 411 | 100001001 |
| 412 | 100001010 |
| 413 | 100001011 |
| 414 | 100001100 |
| 415 | 100001101 |
| 416 | 100001110 |
| 417 | 100001111 |
| 420 | 100010000 |
| 421 | 100010001 |
| 422 | 100010010 |
| 423 | 100010011 |
| 424 | 100010100 |
| 425 | 100010101 |
| 426 | 100010110 |
| 427 | 100010111 |
| 430 | 100011000 |
| 431 | 100011001 |
| 432 | 100011010 |
| 433 | 100011011 |
| 434 | 100011100 |
| 435 | 100011101 |
| 436 | 100011110 |
| 437 | 100011111 |
| 440 | 100100000 |
| 441 | 100100001 |
| 442 | 100100010 |
| 443 | 100100011 |
| 444 | 100100100 |
| 445 | 100100101 |
| 446 | 100100110 |
| 447 | 100100111 |
| 450 | 100101000 |
| 451 | 100101001 |
| 452 | 100101010 |
| 453 | 100101011 |
| 454 | 100101100 |