Convertir de Hexadécimal (Base 16) à Binaire (Base 2)
Effectuez la conversion de nombres entre différents systèmes numériques.
Hexadécimal (Base 16) = Binaire (Base 2)
Informations sur les unités de conversion:
À propos de Hexadécimal (Base 16)
Le système hexadécimal réduit un nombre de huit bits à seulement deux chiffres hexadécimaux. Cela réduit la confusion qui peut survenir en lisant de longues chaînes de nombres binaires et la quantité d'espace nécessaire pour écrire des nombres binaires.
À propos de Binaire (Base 2)
Le système binaire est une technique de numération qui utilise uniquement deux chiffres, 0 et 1. Il est couramment utilisé en informatique. Cette méthode repose uniquement sur deux symboles, le un et le zéro. Tout nombre peut être exprimé à la fois dans le système décimal et binaire.
Hexadécimal (Base 16) vs Binaire (Base 2)
| Hexadécimal (Base 16) | Binaire (Base 2) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| a | 1010 |
| b | 1011 |
| c | 1100 |
| d | 1101 |
| e | 1110 |
| f | 1111 |
¿Comment convertir de Hexadécimal (Base 16) à Binaire (Base 2)?
Remarque : Pour convertir un nombre hexadécimal (base 16) en une autre base, commencez par convertir la valeur hexadécimale en décimal (base 10). Suivez ces étapes :
- Identifiez chaque chiffre du nombre hexadécimal.
- Calculez la position de chaque chiffre. Commencez par le chiffre le plus à droite, qui aura une position de 0. Chaque chiffre à gauche aura une position incrémentielle (1, 2, 3, etc.).
- Calculez la valeur décimale de chaque chiffre en le multipliant par la base (16) élevée à la position du chiffre. Par exemple : chiffre * 16^position.
- additionnez les valeurs obtenues à l'étape précédente pour obtenir le nombre décimal équivalent.
Application de ces étapes au nombre hexadécimal 9F :
- 9 et F sont les chiffres.
- En partant de la droite, les positions sont 0 et 1.
- 9 * 16^1 = 144 ; F (qui vaut 15 en décimal) * 16^0 = 15.
- 144 + 15 = 159 décimal.
Ainsi, 9F hexadécimal = 159 décimal.

Remarque : Pour convertir un nombre décimal (base 10) en nombre binaire (base 2), suivez ces étapes :
- Divisez le nombre décimal par 2 de manière répétée et notez les restes des divisions.
- Le processus se termine lorsque le résultat de la division est égal à 0.
- Les restes des divisions doivent être écrits dans l'ordre inverse car ils représentent les poids des chiffres binaires correspondants.
Application de ces étapes au nombre décimal 159 :
Voici un exemple de conversion du nombre décimal 159 en binaire :
- Divisez 159 par 2 : 159 ÷ 2 = 79 avec un reste de 1.
- Divisez 79 par 2 : 79 ÷ 2 = 39 avec un reste de 1.
- Divisez 39 par 2 : 39 ÷ 2 = 19 avec un reste de 1.
- Divisez 19 par 2 : 19 ÷ 2 = 9 avec un reste de 1.
- Divisez 9 par 2 : 9 ÷ 2 = 4 avec un reste de 1.
- Divisez 4 par 2 : 4 ÷ 2 = 2 avec un reste de 0.
- Divisez 2 par 2 : 2 ÷ 2 = 1 avec un reste de 0.
- Divisez 1 par 2 : 1 ÷ 2 = 0 avec un reste de 1.
Les restes des divisions sont écrits dans l'ordre inverse : 10011111.
Ainsi, le nombre 159 en décimal se convertit en 10011111 en binaire.
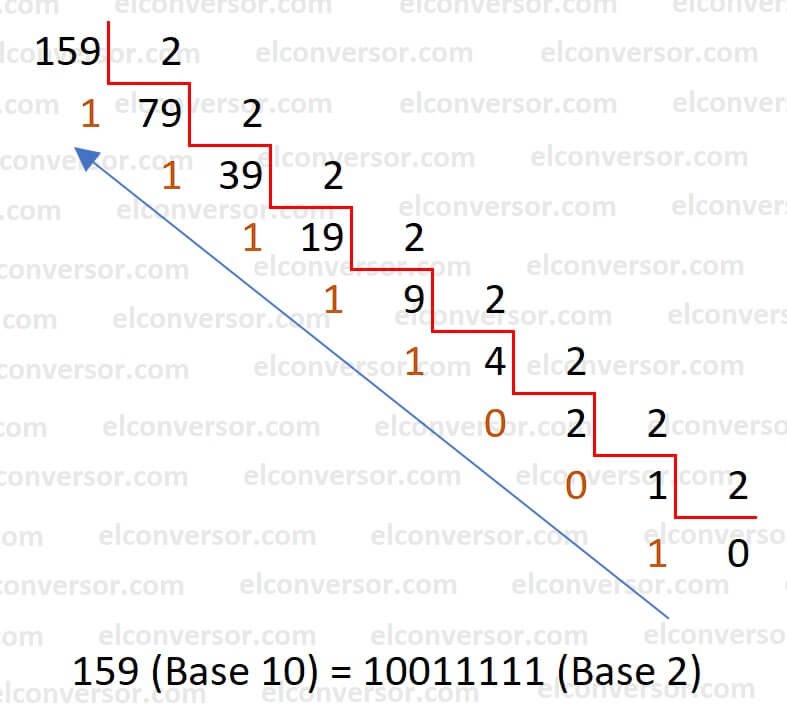
Table de conversion de Hexadécimal (Base 16) à Binaire (Base 2)
| Hexadécimal (Base 16) | Binaire (Base 2) |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| a | 1010 |
| b | 1011 |
| c | 1100 |
| d | 1101 |
| e | 1110 |
| f | 1111 |
| 10 | 10000 |
| 11 | 10001 |
| 12 | 10010 |
| 13 | 10011 |
| 14 | 10100 |
| 15 | 10101 |
| 16 | 10110 |
| 17 | 10111 |
| 18 | 11000 |
| 19 | 11001 |
| 1a | 11010 |
| 1b | 11011 |
| 1c | 11100 |
| 1d | 11101 |
| 1e | 11110 |
| 1f | 11111 |
| 20 | 100000 |
| 21 | 100001 |
| 22 | 100010 |
| 23 | 100011 |
| 24 | 100100 |
| 25 | 100101 |
| 26 | 100110 |
| 27 | 100111 |
| 28 | 101000 |
| 29 | 101001 |
| 2a | 101010 |
| 2b | 101011 |
| 2c | 101100 |
| 2d | 101101 |
| 2e | 101110 |
| 2f | 101111 |
| 30 | 110000 |
| 31 | 110001 |
| 32 | 110010 |
| 33 | 110011 |
| 34 | 110100 |
| 35 | 110101 |
| 36 | 110110 |
| 37 | 110111 |
| 38 | 111000 |
| 39 | 111001 |
| 3a | 111010 |
| 3b | 111011 |
| 3c | 111100 |
| 3d | 111101 |
| 3e | 111110 |
| 3f | 111111 |
| 40 | 1000000 |
| 41 | 1000001 |
| 42 | 1000010 |
| 43 | 1000011 |
| 44 | 1000100 |
| 45 | 1000101 |
| 46 | 1000110 |
| 47 | 1000111 |
| 48 | 1001000 |
| 49 | 1001001 |
| 4a | 1001010 |
| 4b | 1001011 |
| 4c | 1001100 |
| 4d | 1001101 |
| 4e | 1001110 |
| 4f | 1001111 |
| 50 | 1010000 |
| 51 | 1010001 |
| 52 | 1010010 |
| 53 | 1010011 |
| 54 | 1010100 |
| 55 | 1010101 |
| 56 | 1010110 |
| 57 | 1010111 |
| 58 | 1011000 |
| 59 | 1011001 |
| 5a | 1011010 |
| 5b | 1011011 |
| 5c | 1011100 |
| 5d | 1011101 |
| 5e | 1011110 |
| 5f | 1011111 |
| 60 | 1100000 |
| 61 | 1100001 |
| 62 | 1100010 |
| 63 | 1100011 |
| 64 | 1100100 |
| 65 | 1100101 |
| 66 | 1100110 |
| 67 | 1100111 |
| 68 | 1101000 |
| 69 | 1101001 |
| 6a | 1101010 |
| 6b | 1101011 |
| 6c | 1101100 |
| 6d | 1101101 |
| 6e | 1101110 |
| 6f | 1101111 |
| 70 | 1110000 |
| 71 | 1110001 |
| 72 | 1110010 |
| 73 | 1110011 |
| 74 | 1110100 |
| 75 | 1110101 |
| 76 | 1110110 |
| 77 | 1110111 |
| 78 | 1111000 |
| 79 | 1111001 |
| 7a | 1111010 |
| 7b | 1111011 |
| 7c | 1111100 |
| 7d | 1111101 |
| 7e | 1111110 |
| 7f | 1111111 |
| 80 | 10000000 |
| 81 | 10000001 |
| 82 | 10000010 |
| 83 | 10000011 |
| 84 | 10000100 |
| 85 | 10000101 |
| 86 | 10000110 |
| 87 | 10000111 |
| 88 | 10001000 |
| 89 | 10001001 |
| 8a | 10001010 |
| 8b | 10001011 |
| 8c | 10001100 |
| 8d | 10001101 |
| 8e | 10001110 |
| 8f | 10001111 |
| 90 | 10010000 |
| 91 | 10010001 |
| 92 | 10010010 |
| 93 | 10010011 |
| 94 | 10010100 |
| 95 | 10010101 |
| 96 | 10010110 |
| 97 | 10010111 |
| 98 | 10011000 |
| 99 | 10011001 |
| 9a | 10011010 |
| 9b | 10011011 |
| 9c | 10011100 |
| 9d | 10011101 |
| 9e | 10011110 |
| 9f | 10011111 |
| a0 | 10100000 |
| a1 | 10100001 |
| a2 | 10100010 |
| a3 | 10100011 |
| a4 | 10100100 |
| a5 | 10100101 |
| a6 | 10100110 |
| a7 | 10100111 |
| a8 | 10101000 |
| a9 | 10101001 |
| aa | 10101010 |
| ab | 10101011 |
| ac | 10101100 |
| ad | 10101101 |
| ae | 10101110 |
| af | 10101111 |
| b0 | 10110000 |
| b1 | 10110001 |
| b2 | 10110010 |
| b3 | 10110011 |
| b4 | 10110100 |
| b5 | 10110101 |
| b6 | 10110110 |
| b7 | 10110111 |
| b8 | 10111000 |
| b9 | 10111001 |
| ba | 10111010 |
| bb | 10111011 |
| bc | 10111100 |
| bd | 10111101 |
| be | 10111110 |
| bf | 10111111 |
| c0 | 11000000 |
| c1 | 11000001 |
| c2 | 11000010 |
| c3 | 11000011 |
| c4 | 11000100 |
| c5 | 11000101 |
| c6 | 11000110 |
| c7 | 11000111 |
| c8 | 11001000 |
| c9 | 11001001 |
| ca | 11001010 |
| cb | 11001011 |
| cc | 11001100 |
| cd | 11001101 |
| ce | 11001110 |
| cf | 11001111 |
| d0 | 11010000 |
| d1 | 11010001 |
| d2 | 11010010 |
| d3 | 11010011 |
| d4 | 11010100 |
| d5 | 11010101 |
| d6 | 11010110 |
| d7 | 11010111 |
| d8 | 11011000 |
| d9 | 11011001 |
| da | 11011010 |
| db | 11011011 |
| dc | 11011100 |
| dd | 11011101 |
| de | 11011110 |
| df | 11011111 |
| e0 | 11100000 |
| e1 | 11100001 |
| e2 | 11100010 |
| e3 | 11100011 |
| e4 | 11100100 |
| e5 | 11100101 |
| e6 | 11100110 |
| e7 | 11100111 |
| e8 | 11101000 |
| e9 | 11101001 |
| ea | 11101010 |
| eb | 11101011 |
| ec | 11101100 |
| ed | 11101101 |
| ee | 11101110 |
| ef | 11101111 |
| f0 | 11110000 |
| f1 | 11110001 |
| f2 | 11110010 |
| f3 | 11110011 |
| f4 | 11110100 |
| f5 | 11110101 |
| f6 | 11110110 |
| f7 | 11110111 |
| f8 | 11111000 |
| f9 | 11111001 |
| fa | 11111010 |
| fb | 11111011 |
| fc | 11111100 |
| fd | 11111101 |
| fe | 11111110 |
| ff | 11111111 |
| 100 | 100000000 |
| 101 | 100000001 |
| 102 | 100000010 |
| 103 | 100000011 |
| 104 | 100000100 |
| 105 | 100000101 |
| 106 | 100000110 |
| 107 | 100000111 |
| 108 | 100001000 |
| 109 | 100001001 |
| 10a | 100001010 |
| 10b | 100001011 |
| 10c | 100001100 |
| 10d | 100001101 |
| 10e | 100001110 |
| 10f | 100001111 |
| 110 | 100010000 |
| 111 | 100010001 |
| 112 | 100010010 |
| 113 | 100010011 |
| 114 | 100010100 |
| 115 | 100010101 |
| 116 | 100010110 |
| 117 | 100010111 |
| 118 | 100011000 |
| 119 | 100011001 |
| 11a | 100011010 |
| 11b | 100011011 |
| 11c | 100011100 |
| 11d | 100011101 |
| 11e | 100011110 |
| 11f | 100011111 |
| 120 | 100100000 |
| 121 | 100100001 |
| 122 | 100100010 |
| 123 | 100100011 |
| 124 | 100100100 |
| 125 | 100100101 |
| 126 | 100100110 |
| 127 | 100100111 |
| 128 | 100101000 |
| 129 | 100101001 |
| 12a | 100101010 |
| 12b | 100101011 |
| 12c | 100101100 |