Converter de Binário (Base 2) para Romano (Rom)
Realize a conversão de números entre diferentes sistemas numéricos.
Binário (Base 2) = Romano (Rom)
Informações sobre as unidades de conversão:
Sobre Binário (Base 2)
O sistema binário é uma técnica de numeração que utiliza apenas dois dígitos, 0 e 1. É comumente usado em computação. Este método se baseia exclusivamente em dois símbolos, o um e o zero. Qualquer número pode ser expresso tanto no sistema decimal quanto no binário.
Sobre Romano (Rom)
O sistema de numeração romana é um sistema numérico antigo que era usado no Império Romano. Nesse sistema, letras são usadas para representar números, sendo as letras mais comumente usadas: I, V, X, L, C, D e M. Cada letra tem um valor numérico específico, e elas são combinadas de certas maneiras para formar os números. Ao contrário do sistema decimal, o sistema de numeração romana não possui uma representação nativa do zero. Isso significa que não há um símbolo específico para zero no sistema de numeração romana. Apesar disso, o sistema de numeração romana ainda é usado em alguns contextos, como a numeração dos anos em alguns calendários.
Binário (Base 2) vs Romano (Rom)
| Binário (Base 2) | Decimal (Base 10) | Romano (Rom) |
|---|---|---|
| 1 | 1 | I |
| 100 | 4 | IV |
| 101 | 5 | V |
| 1001 | 9 | IX |
| 1010 | 10 | X |
| 101000 | 40 | XL |
| 110010 | 50 | L |
| 1011010 | 90 | XC |
| 1100100 | 100 | C |
| 110010000 | 400 | CD |
| 111110100 | 500 | D |
| 1110000100 | 900 | CM |
| 1111101000 | 1000 | M |
| 111110100000 | 4000 | IV |
| 1001110001000 | 5000 | V |
| 10001100101000 | 9000 | IX |
| 10011100010000 | 10000 | X |
| 1001110001000000 | 40000 | XL |
| 1100001101010000 | 50000 | L |
| 10101111110010000 | 90000 | XC |
| 11000011010100000 | 100000 | C |
| 1100001101010000000 | 400000 | CD |
| 1111010000100100000 | 500000 | D |
| 11011011101110100000 | 900000 | CM |
| 11110100001001000000 | 1000000 | M |
¿Como converter de Binário (Base 2) para Romano (Rom)?
Nota: Para converter um número em binário (base 2) para qualquer outra base, é necessário primeiro converter o valor binário para decimal (base 10). Siga estes passos:
- Identifique cada dígito do número binário.
- Calcule a posição de cada dígito. Comece pelo dígito mais à direita, que terá uma posição de 0. Cada dígito à esquerda terá uma posição incremental de 1 (1, 2, 3, etc.).
- Calcule o valor decimal de cada dígito multiplicando-o pela base (2) elevada à posição do dígito. Por exemplo: dígito * 2^posição.
- Some os valores obtidos no passo anterior para obter o número decimal equivalente.
Aplicando esses passos ao número binário 10011111:
Vamos ver como converter o número binário 10011111 para decimal.
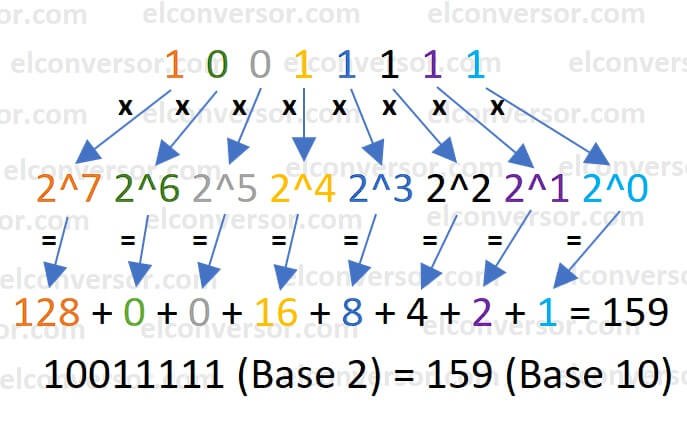
- 1, 0, 0, 1, 1, 1, 1 e 1 são os dígitos.
- Começando pelo mais à direita, as posições são 0, 1, 2, 3, 4, 5, 6 e 7.
- 1 * 2^7 = 128; 0 * 2^6 = 0; 0 * 2^5 = 0; 1 * 2^4 = 16; 1 * 2^3 = 8; 1 * 2^2 = 4; 1 * 2^1 = 2; 1 * 2^0 = 1;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 decimal.
Portanto, 10011111 binário = 159 decimal.
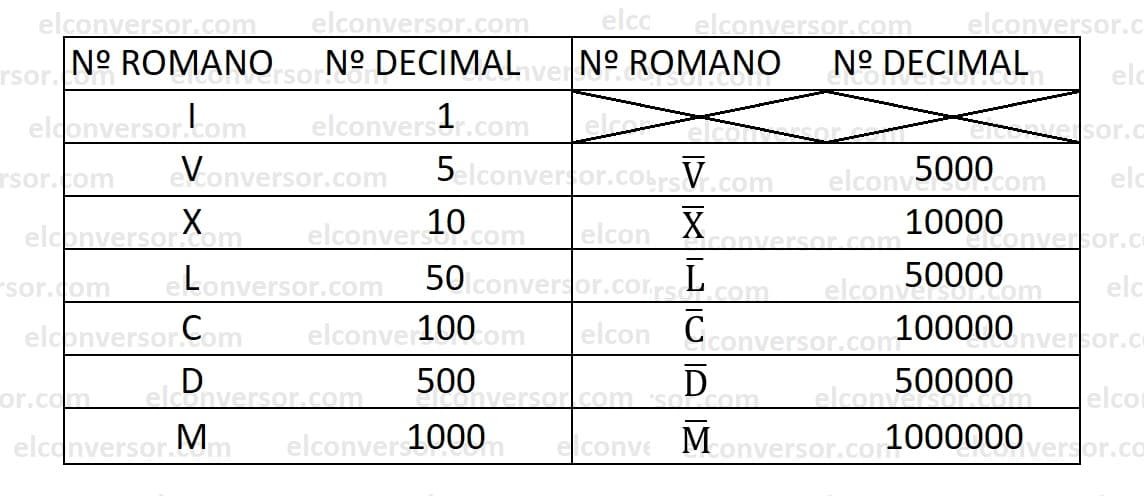
Para converter um número decimal em número romano, é necessário seguir uma série de regras:
Números romanos e suas regras básicas.
- Os números romanos I, X, C e M podem ser repetidos até três vezes ao escrever um número romano composto.
- Os números romanos V, L e D nunca podem ser repetidos.
- Se um número romano composto tem um número menor à direita do que à esquerda, ambos são somados. Exemplo: XI: O número à direita (I = 1) é menor do que à esquerda (X = 10), então eles são somados, ou seja, XI = 11.
- Se um número romano composto tem um número maior à direita e é I, X ou C, então o da esquerda é subtraído do da direita. Exemplo: IX: O número à direita (X = 10) é maior do que à esquerda (I = 1) e é I, então o da esquerda é subtraído do da direita, ou seja, IX = 9.
- Se um número romano tem uma linha sobre ele, seu valor é multiplicado por mil. Exemplo: IX
: o número é 9.000, pois é o número romano que representa 9 e a linha sobre ele o multiplica por mil.
Passos para converter o número decimal 159 em número romano:
- Descomponha o número em unidades, neste caso: 100, 50 e 9.
- Traduza usando a tabela, cada número decimal pelo seu equivalente número romano. Neste caso: C = 100, L = 50 e IX = 9.
- Escreva o resultado da unidade maior para a menor ou da esquerda para a direita: CLIX.
Como resultado, o número decimal 159 é igual a CLIX em números romanos.
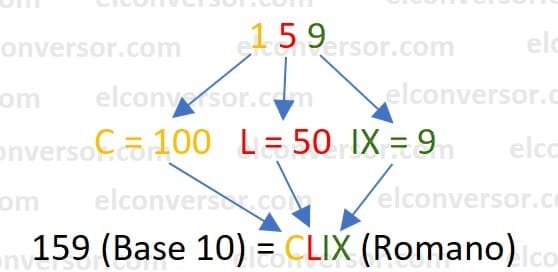
Tabela de conversão de Binário (Base 2) para Romano (Rom)
| Binário (Base 2) | Romano (Rom) |
|---|---|
| 1 | I |
| 10 | II |
| 11 | III |
| 100 | IV |
| 101 | V |
| 110 | VI |
| 111 | VII |
| 1000 | VIII |
| 1001 | IX |
| 1010 | X |
| 1011 | XI |
| 1100 | XII |
| 1101 | XIII |
| 1110 | XIV |
| 1111 | XV |
| 10000 | XVI |
| 10001 | XVII |
| 10010 | XVIII |
| 10011 | XIX |
| 10100 | XX |
| 10101 | XXI |
| 10110 | XXII |
| 10111 | XXIII |
| 11000 | XXIV |
| 11001 | XXV |
| 11010 | XXVI |
| 11011 | XXVII |
| 11100 | XXVIII |
| 11101 | XXIX |
| 11110 | XXX |
| 11111 | XXXI |
| 100000 | XXXII |
| 100001 | XXXIII |
| 100010 | XXXIV |
| 100011 | XXXV |
| 100100 | XXXVI |
| 100101 | XXXVII |
| 100110 | XXXVIII |
| 100111 | XXXIX |
| 101000 | XL |
| 101001 | XLI |
| 101010 | XLII |
| 101011 | XLIII |
| 101100 | XLIV |
| 101101 | XLV |
| 101110 | XLVI |
| 101111 | XLVII |
| 110000 | XLVIII |
| 110001 | XLIX |
| 110010 | L |
| 110011 | LI |
| 110100 | LII |
| 110101 | LIII |
| 110110 | LIV |
| 110111 | LV |
| 111000 | LVI |
| 111001 | LVII |
| 111010 | LVIII |
| 111011 | LIX |
| 111100 | LX |
| 111101 | LXI |
| 111110 | LXII |
| 111111 | LXIII |
| 1000000 | LXIV |
| 1000001 | LXV |
| 1000010 | LXVI |
| 1000011 | LXVII |
| 1000100 | LXVIII |
| 1000101 | LXIX |
| 1000110 | LXX |
| 1000111 | LXXI |
| 1001000 | LXXII |
| 1001001 | LXXIII |
| 1001010 | LXXIV |
| 1001011 | LXXV |
| 1001100 | LXXVI |
| 1001101 | LXXVII |
| 1001110 | LXXVIII |
| 1001111 | LXXIX |
| 1010000 | LXXX |
| 1010001 | LXXXI |
| 1010010 | LXXXII |
| 1010011 | LXXXIII |
| 1010100 | LXXXIV |
| 1010101 | LXXXV |
| 1010110 | LXXXVI |
| 1010111 | LXXXVII |
| 1011000 | LXXXVIII |
| 1011001 | LXXXIX |
| 1011010 | XC |
| 1011011 | XCI |
| 1011100 | XCII |
| 1011101 | XCIII |
| 1011110 | XCIV |
| 1011111 | XCV |
| 1100000 | XCVI |
| 1100001 | XCVII |
| 1100010 | XCVIII |
| 1100011 | XCIX |
| 1100100 | C |
| 1100101 | CI |
| 1100110 | CII |
| 1100111 | CIII |
| 1101000 | CIV |
| 1101001 | CV |
| 1101010 | CVI |
| 1101011 | CVII |
| 1101100 | CVIII |
| 1101101 | CIX |
| 1101110 | CX |
| 1101111 | CXI |
| 1110000 | CXII |
| 1110001 | CXIII |
| 1110010 | CXIV |
| 1110011 | CXV |
| 1110100 | CXVI |
| 1110101 | CXVII |
| 1110110 | CXVIII |
| 1110111 | CXIX |
| 1111000 | CXX |
| 1111001 | CXXI |
| 1111010 | CXXII |
| 1111011 | CXXIII |
| 1111100 | CXXIV |
| 1111101 | CXXV |
| 1111110 | CXXVI |
| 1111111 | CXXVII |
| 10000000 | CXXVIII |
| 10000001 | CXXIX |
| 10000010 | CXXX |
| 10000011 | CXXXI |
| 10000100 | CXXXII |
| 10000101 | CXXXIII |
| 10000110 | CXXXIV |
| 10000111 | CXXXV |
| 10001000 | CXXXVI |
| 10001001 | CXXXVII |
| 10001010 | CXXXVIII |
| 10001011 | CXXXIX |
| 10001100 | CXL |
| 10001101 | CXLI |
| 10001110 | CXLII |
| 10001111 | CXLIII |
| 10010000 | CXLIV |
| 10010001 | CXLV |
| 10010010 | CXLVI |
| 10010011 | CXLVII |
| 10010100 | CXLVIII |
| 10010101 | CXLIX |
| 10010110 | CL |
| 10010111 | CLI |
| 10011000 | CLII |
| 10011001 | CLIII |
| 10011010 | CLIV |
| 10011011 | CLV |
| 10011100 | CLVI |
| 10011101 | CLVII |
| 10011110 | CLVIII |
| 10011111 | CLIX |
| 10100000 | CLX |
| 10100001 | CLXI |
| 10100010 | CLXII |
| 10100011 | CLXIII |
| 10100100 | CLXIV |
| 10100101 | CLXV |
| 10100110 | CLXVI |
| 10100111 | CLXVII |
| 10101000 | CLXVIII |
| 10101001 | CLXIX |
| 10101010 | CLXX |
| 10101011 | CLXXI |
| 10101100 | CLXXII |
| 10101101 | CLXXIII |
| 10101110 | CLXXIV |
| 10101111 | CLXXV |
| 10110000 | CLXXVI |
| 10110001 | CLXXVII |
| 10110010 | CLXXVIII |
| 10110011 | CLXXIX |
| 10110100 | CLXXX |
| 10110101 | CLXXXI |
| 10110110 | CLXXXII |
| 10110111 | CLXXXIII |
| 10111000 | CLXXXIV |
| 10111001 | CLXXXV |
| 10111010 | CLXXXVI |
| 10111011 | CLXXXVII |
| 10111100 | CLXXXVIII |
| 10111101 | CLXXXIX |
| 10111110 | CXC |
| 10111111 | CXCI |
| 11000000 | CXCII |
| 11000001 | CXCIII |
| 11000010 | CXCIV |
| 11000011 | CXCV |
| 11000100 | CXCVI |
| 11000101 | CXCVII |
| 11000110 | CXCVIII |
| 11000111 | CXCIX |
| 11001000 | CC |
| 11001001 | CCI |
| 11001010 | CCII |
| 11001011 | CCIII |
| 11001100 | CCIV |
| 11001101 | CCV |
| 11001110 | CCVI |
| 11001111 | CCVII |
| 11010000 | CCVIII |
| 11010001 | CCIX |
| 11010010 | CCX |
| 11010011 | CCXI |
| 11010100 | CCXII |
| 11010101 | CCXIII |
| 11010110 | CCXIV |
| 11010111 | CCXV |
| 11011000 | CCXVI |
| 11011001 | CCXVII |
| 11011010 | CCXVIII |
| 11011011 | CCXIX |
| 11011100 | CCXX |
| 11011101 | CCXXI |
| 11011110 | CCXXII |
| 11011111 | CCXXIII |
| 11100000 | CCXXIV |
| 11100001 | CCXXV |
| 11100010 | CCXXVI |
| 11100011 | CCXXVII |
| 11100100 | CCXXVIII |
| 11100101 | CCXXIX |
| 11100110 | CCXXX |
| 11100111 | CCXXXI |
| 11101000 | CCXXXII |
| 11101001 | CCXXXIII |
| 11101010 | CCXXXIV |
| 11101011 | CCXXXV |
| 11101100 | CCXXXVI |
| 11101101 | CCXXXVII |
| 11101110 | CCXXXVIII |
| 11101111 | CCXXXIX |
| 11110000 | CCXL |
| 11110001 | CCXLI |
| 11110010 | CCXLII |
| 11110011 | CCXLIII |
| 11110100 | CCXLIV |
| 11110101 | CCXLV |
| 11110110 | CCXLVI |
| 11110111 | CCXLVII |
| 11111000 | CCXLVIII |
| 11111001 | CCXLIX |
| 11111010 | CCL |
| 11111011 | CCLI |
| 11111100 | CCLII |
| 11111101 | CCLIII |
| 11111110 | CCLIV |
| 11111111 | CCLV |
| 100000000 | CCLVI |
| 100000001 | CCLVII |
| 100000010 | CCLVIII |
| 100000011 | CCLIX |
| 100000100 | CCLX |
| 100000101 | CCLXI |
| 100000110 | CCLXII |
| 100000111 | CCLXIII |
| 100001000 | CCLXIV |
| 100001001 | CCLXV |
| 100001010 | CCLXVI |
| 100001011 | CCLXVII |
| 100001100 | CCLXVIII |
| 100001101 | CCLXIX |
| 100001110 | CCLXX |
| 100001111 | CCLXXI |
| 100010000 | CCLXXII |
| 100010001 | CCLXXIII |
| 100010010 | CCLXXIV |
| 100010011 | CCLXXV |
| 100010100 | CCLXXVI |
| 100010101 | CCLXXVII |
| 100010110 | CCLXXVIII |
| 100010111 | CCLXXIX |
| 100011000 | CCLXXX |
| 100011001 | CCLXXXI |
| 100011010 | CCLXXXII |
| 100011011 | CCLXXXIII |
| 100011100 | CCLXXXIV |
| 100011101 | CCLXXXV |
| 100011110 | CCLXXXVI |
| 100011111 | CCLXXXVII |
| 100100000 | CCLXXXVIII |
| 100100001 | CCLXXXIX |
| 100100010 | CCXC |
| 100100011 | CCXCI |
| 100100100 | CCXCII |
| 100100101 | CCXCIII |
| 100100110 | CCXCIV |
| 100100111 | CCXCV |
| 100101000 | CCXCVI |
| 100101001 | CCXCVII |
| 100101010 | CCXCVIII |
| 100101011 | CCXCIX |
| 100101100 | CCC |