Converter de Binário (Base 2) para Hexadecimal (Base 16)
Realize a conversão de números entre diferentes sistemas numéricos.
Binário (Base 2) = Hexadecimal (Base 16)
Informações sobre as unidades de conversão:
Sobre Binário (Base 2)
O sistema binário é uma técnica de numeração que utiliza apenas dois dígitos, 0 e 1. É comumente usado em computação. Este método se baseia exclusivamente em dois símbolos, o um e o zero. Qualquer número pode ser expresso tanto no sistema decimal quanto no binário.
Sobre Hexadecimal (Base 16)
O sistema hexadecimal reduz um número de oito bits para apenas dois dígitos hexadecimais. Isso reduz a confusão que pode surgir ao ler longas sequências de números binários e a quantidade de espaço necessária para escrever números binários.
Binário (Base 2) vs Hexadecimal (Base 16)
| Binário (Base 2) | Hexadecimal (Base 16) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | a |
| 1011 | b |
| 1100 | c |
| 1101 | d |
| 1110 | e |
| 1111 | f |
¿Como converter de Binário (Base 2) para Hexadecimal (Base 16)?
Nota: Para converter um número em binário (base 2) para qualquer outra base, é necessário primeiro converter o valor binário para decimal (base 10). Siga estes passos:
- Identifique cada dígito do número binário.
- Calcule a posição de cada dígito. Comece pelo dígito mais à direita, que terá uma posição de 0. Cada dígito à esquerda terá uma posição incremental de 1 (1, 2, 3, etc.).
- Calcule o valor decimal de cada dígito multiplicando-o pela base (2) elevada à posição do dígito. Por exemplo: dígito * 2^posição.
- Some os valores obtidos no passo anterior para obter o número decimal equivalente.
Aplicando esses passos ao número binário 10011111:
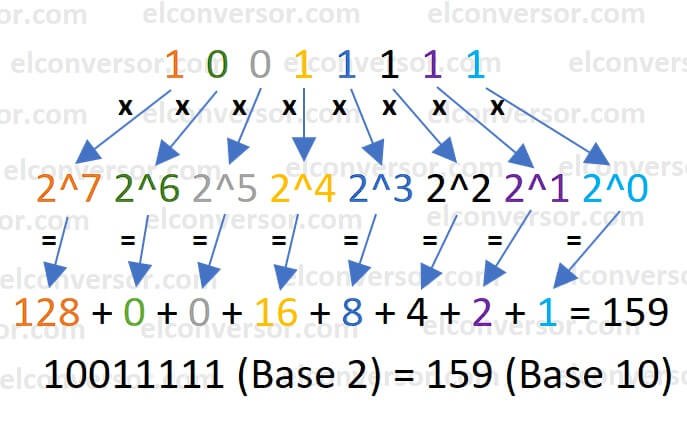
Vamos ver como converter o número binário 10011111 para decimal.
- 1, 0, 0, 1, 1, 1, 1 e 1 são os dígitos.
- Começando pelo mais à direita, as posições são 0, 1, 2, 3, 4, 5, 6 e 7.
- 1 * 2^7 = 128; 0 * 2^6 = 0; 0 * 2^5 = 0; 1 * 2^4 = 16; 1 * 2^3 = 8; 1 * 2^2 = 4; 1 * 2^1 = 2; 1 * 2^0 = 1;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 decimal.
Portanto, 10011111 binário = 159 decimal.
Para converter um número decimal (base 10) em hexadecimal (base 16), siga estas etapas:
- Divida o número decimal por 16.
- Pegue o quociente e divida-o por 16 novamente.
- Repita esse processo até que o quociente seja menor que 16.
- Atribua uma letra a cada resto se o resto for maior que 9.
- Os números 10, 11, 12, 13, 14 e 15 são representados pelas letras A, B, C, D, E e F, respectivamente.
- Escreva os restos obtidos na ordem inversa à qual foram calculados.
Aplicando essas etapas ao número decimal 159:
- 159 / 16 = 9 com um resto de 15.
- 9 / 16 = 0 com um resto de 9.
- 15 é representado como F.
- 9 é representado como 9.

Tabela de conversão de Binário (Base 2) para Hexadecimal (Base 16)
| Binário (Base 2) | Hexadecimal (Base 16) |
|---|---|
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | a |
| 1011 | b |
| 1100 | c |
| 1101 | d |
| 1110 | e |
| 1111 | f |
| 10000 | 10 |
| 10001 | 11 |
| 10010 | 12 |
| 10011 | 13 |
| 10100 | 14 |
| 10101 | 15 |
| 10110 | 16 |
| 10111 | 17 |
| 11000 | 18 |
| 11001 | 19 |
| 11010 | 1a |
| 11011 | 1b |
| 11100 | 1c |
| 11101 | 1d |
| 11110 | 1e |
| 11111 | 1f |
| 100000 | 20 |
| 100001 | 21 |
| 100010 | 22 |
| 100011 | 23 |
| 100100 | 24 |
| 100101 | 25 |
| 100110 | 26 |
| 100111 | 27 |
| 101000 | 28 |
| 101001 | 29 |
| 101010 | 2a |
| 101011 | 2b |
| 101100 | 2c |
| 101101 | 2d |
| 101110 | 2e |
| 101111 | 2f |
| 110000 | 30 |
| 110001 | 31 |
| 110010 | 32 |
| 110011 | 33 |
| 110100 | 34 |
| 110101 | 35 |
| 110110 | 36 |
| 110111 | 37 |
| 111000 | 38 |
| 111001 | 39 |
| 111010 | 3a |
| 111011 | 3b |
| 111100 | 3c |
| 111101 | 3d |
| 111110 | 3e |
| 111111 | 3f |
| 1000000 | 40 |
| 1000001 | 41 |
| 1000010 | 42 |
| 1000011 | 43 |
| 1000100 | 44 |
| 1000101 | 45 |
| 1000110 | 46 |
| 1000111 | 47 |
| 1001000 | 48 |
| 1001001 | 49 |
| 1001010 | 4a |
| 1001011 | 4b |
| 1001100 | 4c |
| 1001101 | 4d |
| 1001110 | 4e |
| 1001111 | 4f |
| 1010000 | 50 |
| 1010001 | 51 |
| 1010010 | 52 |
| 1010011 | 53 |
| 1010100 | 54 |
| 1010101 | 55 |
| 1010110 | 56 |
| 1010111 | 57 |
| 1011000 | 58 |
| 1011001 | 59 |
| 1011010 | 5a |
| 1011011 | 5b |
| 1011100 | 5c |
| 1011101 | 5d |
| 1011110 | 5e |
| 1011111 | 5f |
| 1100000 | 60 |
| 1100001 | 61 |
| 1100010 | 62 |
| 1100011 | 63 |
| 1100100 | 64 |
| 1100101 | 65 |
| 1100110 | 66 |
| 1100111 | 67 |
| 1101000 | 68 |
| 1101001 | 69 |
| 1101010 | 6a |
| 1101011 | 6b |
| 1101100 | 6c |
| 1101101 | 6d |
| 1101110 | 6e |
| 1101111 | 6f |
| 1110000 | 70 |
| 1110001 | 71 |
| 1110010 | 72 |
| 1110011 | 73 |
| 1110100 | 74 |
| 1110101 | 75 |
| 1110110 | 76 |
| 1110111 | 77 |
| 1111000 | 78 |
| 1111001 | 79 |
| 1111010 | 7a |
| 1111011 | 7b |
| 1111100 | 7c |
| 1111101 | 7d |
| 1111110 | 7e |
| 1111111 | 7f |
| 10000000 | 80 |
| 10000001 | 81 |
| 10000010 | 82 |
| 10000011 | 83 |
| 10000100 | 84 |
| 10000101 | 85 |
| 10000110 | 86 |
| 10000111 | 87 |
| 10001000 | 88 |
| 10001001 | 89 |
| 10001010 | 8a |
| 10001011 | 8b |
| 10001100 | 8c |
| 10001101 | 8d |
| 10001110 | 8e |
| 10001111 | 8f |
| 10010000 | 90 |
| 10010001 | 91 |
| 10010010 | 92 |
| 10010011 | 93 |
| 10010100 | 94 |
| 10010101 | 95 |
| 10010110 | 96 |
| 10010111 | 97 |
| 10011000 | 98 |
| 10011001 | 99 |
| 10011010 | 9a |
| 10011011 | 9b |
| 10011100 | 9c |
| 10011101 | 9d |
| 10011110 | 9e |
| 10011111 | 9f |
| 10100000 | a0 |
| 10100001 | a1 |
| 10100010 | a2 |
| 10100011 | a3 |
| 10100100 | a4 |
| 10100101 | a5 |
| 10100110 | a6 |
| 10100111 | a7 |
| 10101000 | a8 |
| 10101001 | a9 |
| 10101010 | aa |
| 10101011 | ab |
| 10101100 | ac |
| 10101101 | ad |
| 10101110 | ae |
| 10101111 | af |
| 10110000 | b0 |
| 10110001 | b1 |
| 10110010 | b2 |
| 10110011 | b3 |
| 10110100 | b4 |
| 10110101 | b5 |
| 10110110 | b6 |
| 10110111 | b7 |
| 10111000 | b8 |
| 10111001 | b9 |
| 10111010 | ba |
| 10111011 | bb |
| 10111100 | bc |
| 10111101 | bd |
| 10111110 | be |
| 10111111 | bf |
| 11000000 | c0 |
| 11000001 | c1 |
| 11000010 | c2 |
| 11000011 | c3 |
| 11000100 | c4 |
| 11000101 | c5 |
| 11000110 | c6 |
| 11000111 | c7 |
| 11001000 | c8 |
| 11001001 | c9 |
| 11001010 | ca |
| 11001011 | cb |
| 11001100 | cc |
| 11001101 | cd |
| 11001110 | ce |
| 11001111 | cf |
| 11010000 | d0 |
| 11010001 | d1 |
| 11010010 | d2 |
| 11010011 | d3 |
| 11010100 | d4 |
| 11010101 | d5 |
| 11010110 | d6 |
| 11010111 | d7 |
| 11011000 | d8 |
| 11011001 | d9 |
| 11011010 | da |
| 11011011 | db |
| 11011100 | dc |
| 11011101 | dd |
| 11011110 | de |
| 11011111 | df |
| 11100000 | e0 |
| 11100001 | e1 |
| 11100010 | e2 |
| 11100011 | e3 |
| 11100100 | e4 |
| 11100101 | e5 |
| 11100110 | e6 |
| 11100111 | e7 |
| 11101000 | e8 |
| 11101001 | e9 |
| 11101010 | ea |
| 11101011 | eb |
| 11101100 | ec |
| 11101101 | ed |
| 11101110 | ee |
| 11101111 | ef |
| 11110000 | f0 |
| 11110001 | f1 |
| 11110010 | f2 |
| 11110011 | f3 |
| 11110100 | f4 |
| 11110101 | f5 |
| 11110110 | f6 |
| 11110111 | f7 |
| 11111000 | f8 |
| 11111001 | f9 |
| 11111010 | fa |
| 11111011 | fb |
| 11111100 | fc |
| 11111101 | fd |
| 11111110 | fe |
| 11111111 | ff |
| 100000000 | 100 |
| 100000001 | 101 |
| 100000010 | 102 |
| 100000011 | 103 |
| 100000100 | 104 |
| 100000101 | 105 |
| 100000110 | 106 |
| 100000111 | 107 |
| 100001000 | 108 |
| 100001001 | 109 |
| 100001010 | 10a |
| 100001011 | 10b |
| 100001100 | 10c |
| 100001101 | 10d |
| 100001110 | 10e |
| 100001111 | 10f |
| 100010000 | 110 |
| 100010001 | 111 |
| 100010010 | 112 |
| 100010011 | 113 |
| 100010100 | 114 |
| 100010101 | 115 |
| 100010110 | 116 |
| 100010111 | 117 |
| 100011000 | 118 |
| 100011001 | 119 |
| 100011010 | 11a |
| 100011011 | 11b |
| 100011100 | 11c |
| 100011101 | 11d |
| 100011110 | 11e |
| 100011111 | 11f |
| 100100000 | 120 |
| 100100001 | 121 |
| 100100010 | 122 |
| 100100011 | 123 |
| 100100100 | 124 |
| 100100101 | 125 |
| 100100110 | 126 |
| 100100111 | 127 |
| 100101000 | 128 |
| 100101001 | 129 |
| 100101010 | 12a |
| 100101011 | 12b |
| 100101100 | 12c |