Convertir de Binaire (Base 2) à Hexadécimal (Base 16)
Effectuez la conversion de nombres entre différents systèmes numériques.
Binaire (Base 2) = Hexadécimal (Base 16)
Informations sur les unités de conversion:
À propos de Binaire (Base 2)
Le système binaire est une technique de numération qui utilise uniquement deux chiffres, 0 et 1. Il est couramment utilisé en informatique. Cette méthode repose uniquement sur deux symboles, le un et le zéro. Tout nombre peut être exprimé à la fois dans le système décimal et binaire.
À propos de Hexadécimal (Base 16)
Le système hexadécimal réduit un nombre de huit bits à seulement deux chiffres hexadécimaux. Cela réduit la confusion qui peut survenir en lisant de longues chaînes de nombres binaires et la quantité d'espace nécessaire pour écrire des nombres binaires.
Binaire (Base 2) vs Hexadécimal (Base 16)
| Binaire (Base 2) | Hexadécimal (Base 16) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | a |
| 1011 | b |
| 1100 | c |
| 1101 | d |
| 1110 | e |
| 1111 | f |
¿Comment convertir de Binaire (Base 2) à Hexadécimal (Base 16)?
Remarque : Pour convertir un nombre binaire (base 2) en toute autre base, il est nécessaire de convertir d'abord la valeur binaire en décimal (base 10). Suivez ces étapes :
- Identifiez chaque chiffre du nombre binaire.
- Calculez la position de chaque chiffre. Commencez par le chiffre le plus à droite, qui aura une position de 0. Chaque chiffre à gauche aura une position incrémentale de 1 (1, 2, 3, etc.).
- Calculez la valeur décimale de chaque chiffre en le multipliant par la base (2) élevée à la position du chiffre. Par exemple : chiffre * 2^position.
- Additionnez les valeurs obtenues à l'étape précédente pour obtenir le nombre décimal équivalent.
Application de ces étapes au nombre binaire 10011111 :
Voyons comment convertir le nombre binaire 10011111 en décimal.
- 1, 0, 0, 1, 1, 1, 1 et 1 sont les chiffres.
- En partant de la droite, les positions sont 0, 1, 2, 3, 4, 5, 6 et 7.
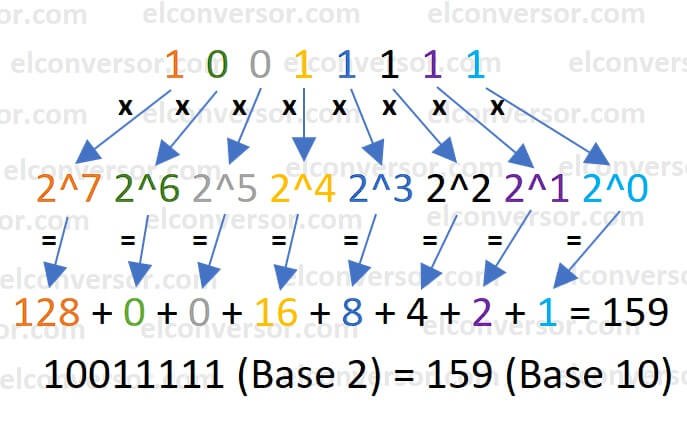
- 1 * 2^7 = 128 ; 0 * 2^6 = 0 ; 0 * 2^5 = 0 ; 1 * 2^4 = 16 ; 1 * 2^3 = 8 ; 1 * 2^2 = 4 ; 1 * 2^1 = 2 ; 1 * 2^0 = 1 ;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 décimal.
Ainsi, 10011111 binaire = 159 décimal.
Pour convertir un nombre décimal (base 10) en hexadécimal (base 16), suivez ces étapes :
- Divisez le nombre décimal par 16.
- Prenez le quotient et divisez-le à nouveau par 16.
- Répétez ce processus jusqu'à ce que le quotient soit inférieur à 16.
- Attribuez une lettre à chaque reste si le reste est supérieur à 9.
- Les nombres 10, 11, 12, 13, 14 et 15 sont représentés par les lettres A, B, C, D, E et F, respectivement.
- Notez les restes obtenus dans l'ordre inverse de leur calcul.
Application de ces étapes au nombre décimal 159 :
- 159 / 16 = 9 avec un reste de 15.
- 9 / 16 = 0 avec un reste de 9.
- 15 est représenté par F.
- 9 est représenté par 9.

Table de conversion de Binaire (Base 2) à Hexadécimal (Base 16)
| Binaire (Base 2) | Hexadécimal (Base 16) |
|---|---|
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | a |
| 1011 | b |
| 1100 | c |
| 1101 | d |
| 1110 | e |
| 1111 | f |
| 10000 | 10 |
| 10001 | 11 |
| 10010 | 12 |
| 10011 | 13 |
| 10100 | 14 |
| 10101 | 15 |
| 10110 | 16 |
| 10111 | 17 |
| 11000 | 18 |
| 11001 | 19 |
| 11010 | 1a |
| 11011 | 1b |
| 11100 | 1c |
| 11101 | 1d |
| 11110 | 1e |
| 11111 | 1f |
| 100000 | 20 |
| 100001 | 21 |
| 100010 | 22 |
| 100011 | 23 |
| 100100 | 24 |
| 100101 | 25 |
| 100110 | 26 |
| 100111 | 27 |
| 101000 | 28 |
| 101001 | 29 |
| 101010 | 2a |
| 101011 | 2b |
| 101100 | 2c |
| 101101 | 2d |
| 101110 | 2e |
| 101111 | 2f |
| 110000 | 30 |
| 110001 | 31 |
| 110010 | 32 |
| 110011 | 33 |
| 110100 | 34 |
| 110101 | 35 |
| 110110 | 36 |
| 110111 | 37 |
| 111000 | 38 |
| 111001 | 39 |
| 111010 | 3a |
| 111011 | 3b |
| 111100 | 3c |
| 111101 | 3d |
| 111110 | 3e |
| 111111 | 3f |
| 1000000 | 40 |
| 1000001 | 41 |
| 1000010 | 42 |
| 1000011 | 43 |
| 1000100 | 44 |
| 1000101 | 45 |
| 1000110 | 46 |
| 1000111 | 47 |
| 1001000 | 48 |
| 1001001 | 49 |
| 1001010 | 4a |
| 1001011 | 4b |
| 1001100 | 4c |
| 1001101 | 4d |
| 1001110 | 4e |
| 1001111 | 4f |
| 1010000 | 50 |
| 1010001 | 51 |
| 1010010 | 52 |
| 1010011 | 53 |
| 1010100 | 54 |
| 1010101 | 55 |
| 1010110 | 56 |
| 1010111 | 57 |
| 1011000 | 58 |
| 1011001 | 59 |
| 1011010 | 5a |
| 1011011 | 5b |
| 1011100 | 5c |
| 1011101 | 5d |
| 1011110 | 5e |
| 1011111 | 5f |
| 1100000 | 60 |
| 1100001 | 61 |
| 1100010 | 62 |
| 1100011 | 63 |
| 1100100 | 64 |
| 1100101 | 65 |
| 1100110 | 66 |
| 1100111 | 67 |
| 1101000 | 68 |
| 1101001 | 69 |
| 1101010 | 6a |
| 1101011 | 6b |
| 1101100 | 6c |
| 1101101 | 6d |
| 1101110 | 6e |
| 1101111 | 6f |
| 1110000 | 70 |
| 1110001 | 71 |
| 1110010 | 72 |
| 1110011 | 73 |
| 1110100 | 74 |
| 1110101 | 75 |
| 1110110 | 76 |
| 1110111 | 77 |
| 1111000 | 78 |
| 1111001 | 79 |
| 1111010 | 7a |
| 1111011 | 7b |
| 1111100 | 7c |
| 1111101 | 7d |
| 1111110 | 7e |
| 1111111 | 7f |
| 10000000 | 80 |
| 10000001 | 81 |
| 10000010 | 82 |
| 10000011 | 83 |
| 10000100 | 84 |
| 10000101 | 85 |
| 10000110 | 86 |
| 10000111 | 87 |
| 10001000 | 88 |
| 10001001 | 89 |
| 10001010 | 8a |
| 10001011 | 8b |
| 10001100 | 8c |
| 10001101 | 8d |
| 10001110 | 8e |
| 10001111 | 8f |
| 10010000 | 90 |
| 10010001 | 91 |
| 10010010 | 92 |
| 10010011 | 93 |
| 10010100 | 94 |
| 10010101 | 95 |
| 10010110 | 96 |
| 10010111 | 97 |
| 10011000 | 98 |
| 10011001 | 99 |
| 10011010 | 9a |
| 10011011 | 9b |
| 10011100 | 9c |
| 10011101 | 9d |
| 10011110 | 9e |
| 10011111 | 9f |
| 10100000 | a0 |
| 10100001 | a1 |
| 10100010 | a2 |
| 10100011 | a3 |
| 10100100 | a4 |
| 10100101 | a5 |
| 10100110 | a6 |
| 10100111 | a7 |
| 10101000 | a8 |
| 10101001 | a9 |
| 10101010 | aa |
| 10101011 | ab |
| 10101100 | ac |
| 10101101 | ad |
| 10101110 | ae |
| 10101111 | af |
| 10110000 | b0 |
| 10110001 | b1 |
| 10110010 | b2 |
| 10110011 | b3 |
| 10110100 | b4 |
| 10110101 | b5 |
| 10110110 | b6 |
| 10110111 | b7 |
| 10111000 | b8 |
| 10111001 | b9 |
| 10111010 | ba |
| 10111011 | bb |
| 10111100 | bc |
| 10111101 | bd |
| 10111110 | be |
| 10111111 | bf |
| 11000000 | c0 |
| 11000001 | c1 |
| 11000010 | c2 |
| 11000011 | c3 |
| 11000100 | c4 |
| 11000101 | c5 |
| 11000110 | c6 |
| 11000111 | c7 |
| 11001000 | c8 |
| 11001001 | c9 |
| 11001010 | ca |
| 11001011 | cb |
| 11001100 | cc |
| 11001101 | cd |
| 11001110 | ce |
| 11001111 | cf |
| 11010000 | d0 |
| 11010001 | d1 |
| 11010010 | d2 |
| 11010011 | d3 |
| 11010100 | d4 |
| 11010101 | d5 |
| 11010110 | d6 |
| 11010111 | d7 |
| 11011000 | d8 |
| 11011001 | d9 |
| 11011010 | da |
| 11011011 | db |
| 11011100 | dc |
| 11011101 | dd |
| 11011110 | de |
| 11011111 | df |
| 11100000 | e0 |
| 11100001 | e1 |
| 11100010 | e2 |
| 11100011 | e3 |
| 11100100 | e4 |
| 11100101 | e5 |
| 11100110 | e6 |
| 11100111 | e7 |
| 11101000 | e8 |
| 11101001 | e9 |
| 11101010 | ea |
| 11101011 | eb |
| 11101100 | ec |
| 11101101 | ed |
| 11101110 | ee |
| 11101111 | ef |
| 11110000 | f0 |
| 11110001 | f1 |
| 11110010 | f2 |
| 11110011 | f3 |
| 11110100 | f4 |
| 11110101 | f5 |
| 11110110 | f6 |
| 11110111 | f7 |
| 11111000 | f8 |
| 11111001 | f9 |
| 11111010 | fa |
| 11111011 | fb |
| 11111100 | fc |
| 11111101 | fd |
| 11111110 | fe |
| 11111111 | ff |
| 100000000 | 100 |
| 100000001 | 101 |
| 100000010 | 102 |
| 100000011 | 103 |
| 100000100 | 104 |
| 100000101 | 105 |
| 100000110 | 106 |
| 100000111 | 107 |
| 100001000 | 108 |
| 100001001 | 109 |
| 100001010 | 10a |
| 100001011 | 10b |
| 100001100 | 10c |
| 100001101 | 10d |
| 100001110 | 10e |
| 100001111 | 10f |
| 100010000 | 110 |
| 100010001 | 111 |
| 100010010 | 112 |
| 100010011 | 113 |
| 100010100 | 114 |
| 100010101 | 115 |
| 100010110 | 116 |
| 100010111 | 117 |
| 100011000 | 118 |
| 100011001 | 119 |
| 100011010 | 11a |
| 100011011 | 11b |
| 100011100 | 11c |
| 100011101 | 11d |
| 100011110 | 11e |
| 100011111 | 11f |
| 100100000 | 120 |
| 100100001 | 121 |
| 100100010 | 122 |
| 100100011 | 123 |
| 100100100 | 124 |
| 100100101 | 125 |
| 100100110 | 126 |
| 100100111 | 127 |
| 100101000 | 128 |
| 100101001 | 129 |
| 100101010 | 12a |
| 100101011 | 12b |
| 100101100 | 12c |