Convert from Octal (Base 8) to Binary (Base 2)
Perform the conversion of numbers between different numerical systems.
Octal (Base 8) = Binary (Base 2)
Information about conversion units:
About Octal (Base 8)
The octal system is the positional numeral system with a base of 8, using the Arabic-Indic digits: 0, 1, 2, 3, 4, 5, 6, 7. In computing, octal numbering is sometimes used instead of hexadecimal. It has the advantage of not requiring symbols other than digits.
About Binary (Base 2)
The binary system is a numbering technique that uses only two digits, 0 and 1. It is commonly used in computing. This method relies solely on two symbols, the one and the zero. Any number can be expressed in both the decimal and binary systems.
Octal (Base 8) vs Binary (Base 2)
| Octal (Base 8) | Binary (Base 2) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
¿How to convert from Octal (Base 8) to Binary (Base 2)?
Note: To convert a number from octal (base 8) to any other base, we first need to convert the octal value to decimal (base 10). To do this, follow these steps:
- Identify each digit of the octal number.
- Calculate the position of each digit. Start from the rightmost digit, which will have a position of 0. Each digit to the left will have an incremental position of 1 (1, 2, 3, etc.).
- Calculate the decimal value of each digit by multiplying it by the base (8) raised to the position of the digit. For example: digit * 8^position.
- Add up the values obtained in the previous step to get the equivalent decimal number.
Applying these steps to the octal number 237:
- 2, 3, and 7 are the digits.
- From right to left, the positions are 0, 1, and 2.
- 2 * 8^2 = 128; 3 * 8^1 = 24; 7 * 8^0 = 7.
- 128 + 24 + 7 = 159 decimal
Therefore, 237 octal = 159 decimal.

Note: To convert a decimal number (base 10) to binary number (base 2), follow these steps:
- Repeatedly divide the decimal number by 2 and record the remainders of the divisions.
- The process ends when the result of the division is 0.
- The remainders of the divisions must be written in reverse order as they represent the weights of the corresponding binary digits.
Applying these steps to the decimal number 159:
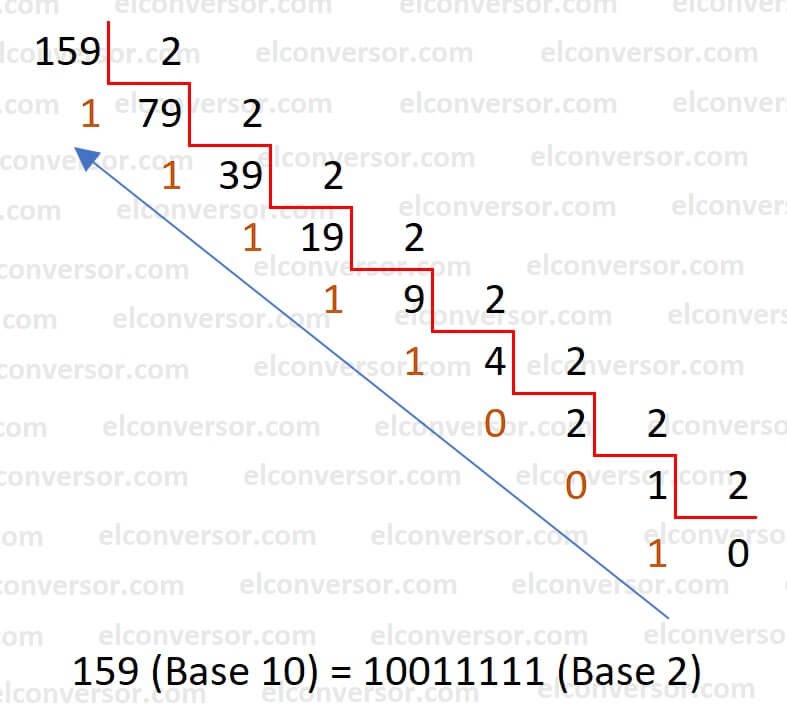
Below is an example of how to convert the decimal number 159 to binary:
- Divide 159 by 2: 159 ÷ 2 = 79 with a remainder of 1.
- Divide 79 by 2: 79 ÷ 2 = 39 with a remainder of 1.
- Divide 39 by 2: 39 ÷ 2 = 19 with a remainder of 1.
- Divide 19 by 2: 19 ÷ 2 = 9 with a remainder of 1.
- Divide 9 by 2: 9 ÷ 2 = 4 with a remainder of 1.
- Divide 4 by 2: 4 ÷ 2 = 2 with a remainder of 0.
- Divide 2 by 2: 2 ÷ 2 = 1 with a remainder of 0.
- Divide 1 by 2: 1 ÷ 2 = 0 with a remainder of 1.
The remainders of the divisions are written in reverse order: 10011111.
Therefore, the number 159 in decimal converts to 10011111 in binary.
Conversion table of Octal (Base 8) to Binary (Base 2)
| Octal (Base 8) | Binary (Base 2) |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 10 | 1000 |
| 11 | 1001 |
| 12 | 1010 |
| 13 | 1011 |
| 14 | 1100 |
| 15 | 1101 |
| 16 | 1110 |
| 17 | 1111 |
| 20 | 10000 |
| 21 | 10001 |
| 22 | 10010 |
| 23 | 10011 |
| 24 | 10100 |
| 25 | 10101 |
| 26 | 10110 |
| 27 | 10111 |
| 30 | 11000 |
| 31 | 11001 |
| 32 | 11010 |
| 33 | 11011 |
| 34 | 11100 |
| 35 | 11101 |
| 36 | 11110 |
| 37 | 11111 |
| 40 | 100000 |
| 41 | 100001 |
| 42 | 100010 |
| 43 | 100011 |
| 44 | 100100 |
| 45 | 100101 |
| 46 | 100110 |
| 47 | 100111 |
| 50 | 101000 |
| 51 | 101001 |
| 52 | 101010 |
| 53 | 101011 |
| 54 | 101100 |
| 55 | 101101 |
| 56 | 101110 |
| 57 | 101111 |
| 60 | 110000 |
| 61 | 110001 |
| 62 | 110010 |
| 63 | 110011 |
| 64 | 110100 |
| 65 | 110101 |
| 66 | 110110 |
| 67 | 110111 |
| 70 | 111000 |
| 71 | 111001 |
| 72 | 111010 |
| 73 | 111011 |
| 74 | 111100 |
| 75 | 111101 |
| 76 | 111110 |
| 77 | 111111 |
| 100 | 1000000 |
| 101 | 1000001 |
| 102 | 1000010 |
| 103 | 1000011 |
| 104 | 1000100 |
| 105 | 1000101 |
| 106 | 1000110 |
| 107 | 1000111 |
| 110 | 1001000 |
| 111 | 1001001 |
| 112 | 1001010 |
| 113 | 1001011 |
| 114 | 1001100 |
| 115 | 1001101 |
| 116 | 1001110 |
| 117 | 1001111 |
| 120 | 1010000 |
| 121 | 1010001 |
| 122 | 1010010 |
| 123 | 1010011 |
| 124 | 1010100 |
| 125 | 1010101 |
| 126 | 1010110 |
| 127 | 1010111 |
| 130 | 1011000 |
| 131 | 1011001 |
| 132 | 1011010 |
| 133 | 1011011 |
| 134 | 1011100 |
| 135 | 1011101 |
| 136 | 1011110 |
| 137 | 1011111 |
| 140 | 1100000 |
| 141 | 1100001 |
| 142 | 1100010 |
| 143 | 1100011 |
| 144 | 1100100 |
| 145 | 1100101 |
| 146 | 1100110 |
| 147 | 1100111 |
| 150 | 1101000 |
| 151 | 1101001 |
| 152 | 1101010 |
| 153 | 1101011 |
| 154 | 1101100 |
| 155 | 1101101 |
| 156 | 1101110 |
| 157 | 1101111 |
| 160 | 1110000 |
| 161 | 1110001 |
| 162 | 1110010 |
| 163 | 1110011 |
| 164 | 1110100 |
| 165 | 1110101 |
| 166 | 1110110 |
| 167 | 1110111 |
| 170 | 1111000 |
| 171 | 1111001 |
| 172 | 1111010 |
| 173 | 1111011 |
| 174 | 1111100 |
| 175 | 1111101 |
| 176 | 1111110 |
| 177 | 1111111 |
| 200 | 10000000 |
| 201 | 10000001 |
| 202 | 10000010 |
| 203 | 10000011 |
| 204 | 10000100 |
| 205 | 10000101 |
| 206 | 10000110 |
| 207 | 10000111 |
| 210 | 10001000 |
| 211 | 10001001 |
| 212 | 10001010 |
| 213 | 10001011 |
| 214 | 10001100 |
| 215 | 10001101 |
| 216 | 10001110 |
| 217 | 10001111 |
| 220 | 10010000 |
| 221 | 10010001 |
| 222 | 10010010 |
| 223 | 10010011 |
| 224 | 10010100 |
| 225 | 10010101 |
| 226 | 10010110 |
| 227 | 10010111 |
| 230 | 10011000 |
| 231 | 10011001 |
| 232 | 10011010 |
| 233 | 10011011 |
| 234 | 10011100 |
| 235 | 10011101 |
| 236 | 10011110 |
| 237 | 10011111 |
| 240 | 10100000 |
| 241 | 10100001 |
| 242 | 10100010 |
| 243 | 10100011 |
| 244 | 10100100 |
| 245 | 10100101 |
| 246 | 10100110 |
| 247 | 10100111 |
| 250 | 10101000 |
| 251 | 10101001 |
| 252 | 10101010 |
| 253 | 10101011 |
| 254 | 10101100 |
| 255 | 10101101 |
| 256 | 10101110 |
| 257 | 10101111 |
| 260 | 10110000 |
| 261 | 10110001 |
| 262 | 10110010 |
| 263 | 10110011 |
| 264 | 10110100 |
| 265 | 10110101 |
| 266 | 10110110 |
| 267 | 10110111 |
| 270 | 10111000 |
| 271 | 10111001 |
| 272 | 10111010 |
| 273 | 10111011 |
| 274 | 10111100 |
| 275 | 10111101 |
| 276 | 10111110 |
| 277 | 10111111 |
| 300 | 11000000 |
| 301 | 11000001 |
| 302 | 11000010 |
| 303 | 11000011 |
| 304 | 11000100 |
| 305 | 11000101 |
| 306 | 11000110 |
| 307 | 11000111 |
| 310 | 11001000 |
| 311 | 11001001 |
| 312 | 11001010 |
| 313 | 11001011 |
| 314 | 11001100 |
| 315 | 11001101 |
| 316 | 11001110 |
| 317 | 11001111 |
| 320 | 11010000 |
| 321 | 11010001 |
| 322 | 11010010 |
| 323 | 11010011 |
| 324 | 11010100 |
| 325 | 11010101 |
| 326 | 11010110 |
| 327 | 11010111 |
| 330 | 11011000 |
| 331 | 11011001 |
| 332 | 11011010 |
| 333 | 11011011 |
| 334 | 11011100 |
| 335 | 11011101 |
| 336 | 11011110 |
| 337 | 11011111 |
| 340 | 11100000 |
| 341 | 11100001 |
| 342 | 11100010 |
| 343 | 11100011 |
| 344 | 11100100 |
| 345 | 11100101 |
| 346 | 11100110 |
| 347 | 11100111 |
| 350 | 11101000 |
| 351 | 11101001 |
| 352 | 11101010 |
| 353 | 11101011 |
| 354 | 11101100 |
| 355 | 11101101 |
| 356 | 11101110 |
| 357 | 11101111 |
| 360 | 11110000 |
| 361 | 11110001 |
| 362 | 11110010 |
| 363 | 11110011 |
| 364 | 11110100 |
| 365 | 11110101 |
| 366 | 11110110 |
| 367 | 11110111 |
| 370 | 11111000 |
| 371 | 11111001 |
| 372 | 11111010 |
| 373 | 11111011 |
| 374 | 11111100 |
| 375 | 11111101 |
| 376 | 11111110 |
| 377 | 11111111 |
| 400 | 100000000 |
| 401 | 100000001 |
| 402 | 100000010 |
| 403 | 100000011 |
| 404 | 100000100 |
| 405 | 100000101 |
| 406 | 100000110 |
| 407 | 100000111 |
| 410 | 100001000 |
| 411 | 100001001 |
| 412 | 100001010 |
| 413 | 100001011 |
| 414 | 100001100 |
| 415 | 100001101 |
| 416 | 100001110 |
| 417 | 100001111 |
| 420 | 100010000 |
| 421 | 100010001 |
| 422 | 100010010 |
| 423 | 100010011 |
| 424 | 100010100 |
| 425 | 100010101 |
| 426 | 100010110 |
| 427 | 100010111 |
| 430 | 100011000 |
| 431 | 100011001 |
| 432 | 100011010 |
| 433 | 100011011 |
| 434 | 100011100 |
| 435 | 100011101 |
| 436 | 100011110 |
| 437 | 100011111 |
| 440 | 100100000 |
| 441 | 100100001 |
| 442 | 100100010 |
| 443 | 100100011 |
| 444 | 100100100 |
| 445 | 100100101 |
| 446 | 100100110 |
| 447 | 100100111 |
| 450 | 100101000 |
| 451 | 100101001 |
| 452 | 100101010 |
| 453 | 100101011 |
| 454 | 100101100 |