Convert from Binary (Base 2) to Roman (Rom)
Perform the conversion of numbers between different numerical systems.
Binary (Base 2) = Roman (Rom)
Information about conversion units:
About Binary (Base 2)
The binary system is a numbering technique that uses only two digits, 0 and 1. It is commonly used in computing. This method relies solely on two symbols, the one and the zero. Any number can be expressed in both the decimal and binary systems.
About Roman (Rom)
The Roman numeral system is an ancient numeric system that was used in the Roman Empire. In this system, letters are used to represent numbers, with the most commonly used letters being I, V, X, L, C, D, and M. Each letter has a specific numeric value, and they are combined in certain ways to form numbers. Unlike the decimal system, the Roman numeral system doesn't have a native representation of zero. That means there is no specific symbol for zero in the Roman numeral system. Despite this, the Roman numeral system is still used in some contexts, such as numbering years in certain calendars.
Binary (Base 2) vs Roman (Rom)
| Binary (Base 2) | Decimal (Base 10) | Roman (Rom) |
|---|---|---|
| 1 | 1 | I |
| 100 | 4 | IV |
| 101 | 5 | V |
| 1001 | 9 | IX |
| 1010 | 10 | X |
| 101000 | 40 | XL |
| 110010 | 50 | L |
| 1011010 | 90 | XC |
| 1100100 | 100 | C |
| 110010000 | 400 | CD |
| 111110100 | 500 | D |
| 1110000100 | 900 | CM |
| 1111101000 | 1000 | M |
| 111110100000 | 4000 | IV |
| 1001110001000 | 5000 | V |
| 10001100101000 | 9000 | IX |
| 10011100010000 | 10000 | X |
| 1001110001000000 | 40000 | XL |
| 1100001101010000 | 50000 | L |
| 10101111110010000 | 90000 | XC |
| 11000011010100000 | 100000 | C |
| 1100001101010000000 | 400000 | CD |
| 1111010000100100000 | 500000 | D |
| 11011011101110100000 | 900000 | CM |
| 11110100001001000000 | 1000000 | M |
¿How to convert from Binary (Base 2) to Roman (Rom)?
Note: To convert a number in binary (base 2) to any other base, we must first convert the binary value to decimal (base 10). Follow these steps:
- Identify each digit of the binary number.
- Calculate the position of each digit. Start from the rightmost digit, which will have a position of 0. Each digit to the left will have an incremental position of 1 (1, 2, 3, etc.).
- Calculate the decimal value of each digit by multiplying it by the base (2) raised to the position of the digit. For example: digit * 2^position.
- Add up the values obtained in the previous step to get the equivalent decimal number.
Applying these steps to the binary number 10011111:
Let's see how to convert the binary number 10011111 to decimal.
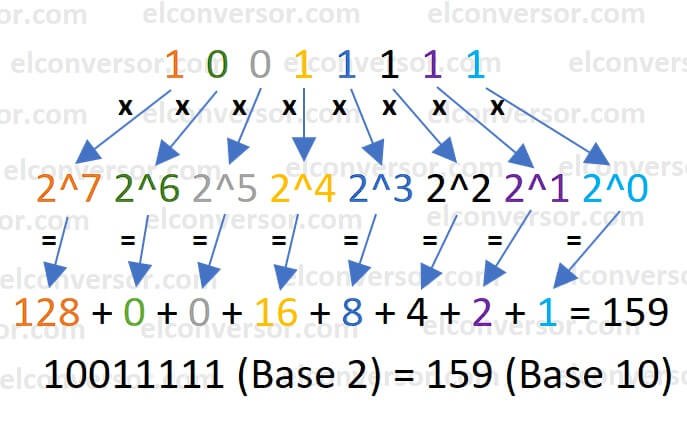
- 1, 0, 0, 1, 1, 1, 1, and 1 are the digits.
- Starting from the rightmost, the positions are 0, 1, 2, 3, 4, 5, 6, and 7.
- 1 * 2^7 = 128; 0 * 2^6 = 0; 0 * 2^5 = 0; 1 * 2^4 = 16; 1 * 2^3 = 8; 1 * 2^2 = 4; 1 * 2^1 = 2; 1 * 2^0 = 1;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 decimal.
Therefore, 10011111 binary = 159 decimal.
To convert a decimal number to a Roman numeral, you need to follow a series of rules:
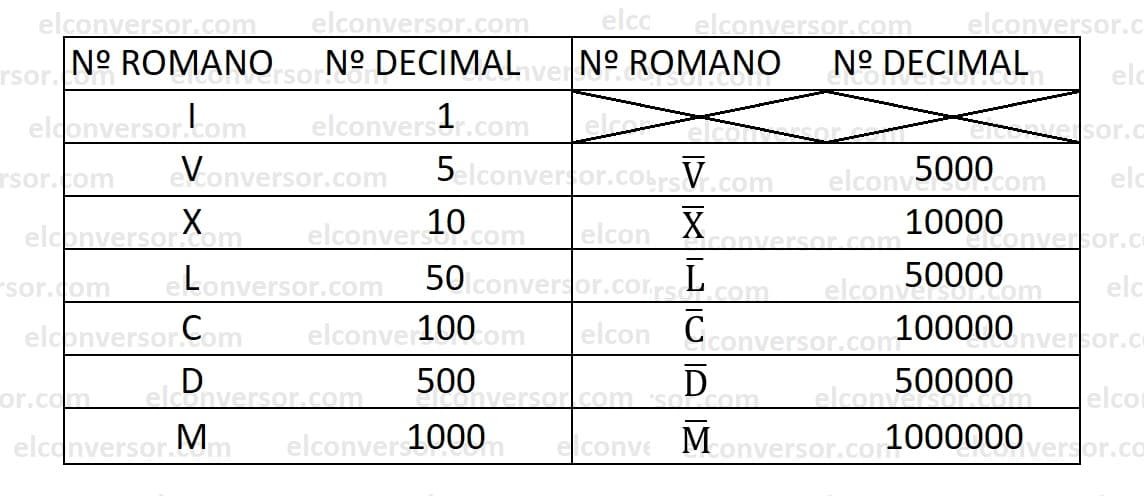
Roman Numerals and Their Basic Rules.
- The Roman numerals I, X, C, and M can be repeated up to three times when writing a composite Roman numeral.
- The Roman numerals V, L, and D cannot be repeated.
- If a composite Roman numeral has a smaller number to the right than to the left, then both are added. Example: XI: The number on the right (I = 1) is smaller than on the left (X = 10), so they are added, i.e., XI = 11.
- If a composite Roman numeral has a larger number to the right and it is I, X, or C, then the left is subtracted from the right. Example: IX: The number on the right (X = 10) is larger than on the left (I = 1), and it's I, so the left is subtracted from the right, i.e., IX = 9.
- If a Roman numeral has a line over it, its value is multiplied by a thousand. Example: IX
: the number is 9,000, as it's the Roman numeral representing 9 and the line over it multiplies it by a thousand.
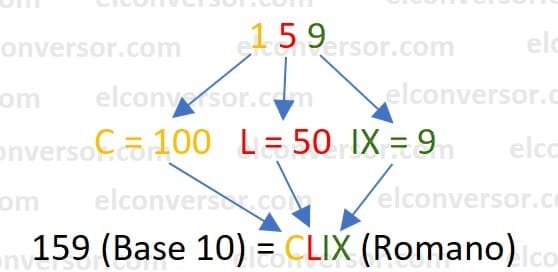
Steps to convert the decimal number 159 into a Roman numeral:
- Break down the number into units, in this case: 100, 50, and 9.
- Translate using the table, each decimal number to its equivalent Roman numeral. In this case: C=100, L=50, and IX=9.
- Write the result from largest to smallest unit or from left to right: CLIX.
As a result, the decimal number 159 is equal to CLIX in Roman numerals.
Conversion table of Binary (Base 2) to Roman (Rom)
| Binary (Base 2) | Roman (Rom) |
|---|---|
| 1 | I |
| 10 | II |
| 11 | III |
| 100 | IV |
| 101 | V |
| 110 | VI |
| 111 | VII |
| 1000 | VIII |
| 1001 | IX |
| 1010 | X |
| 1011 | XI |
| 1100 | XII |
| 1101 | XIII |
| 1110 | XIV |
| 1111 | XV |
| 10000 | XVI |
| 10001 | XVII |
| 10010 | XVIII |
| 10011 | XIX |
| 10100 | XX |
| 10101 | XXI |
| 10110 | XXII |
| 10111 | XXIII |
| 11000 | XXIV |
| 11001 | XXV |
| 11010 | XXVI |
| 11011 | XXVII |
| 11100 | XXVIII |
| 11101 | XXIX |
| 11110 | XXX |
| 11111 | XXXI |
| 100000 | XXXII |
| 100001 | XXXIII |
| 100010 | XXXIV |
| 100011 | XXXV |
| 100100 | XXXVI |
| 100101 | XXXVII |
| 100110 | XXXVIII |
| 100111 | XXXIX |
| 101000 | XL |
| 101001 | XLI |
| 101010 | XLII |
| 101011 | XLIII |
| 101100 | XLIV |
| 101101 | XLV |
| 101110 | XLVI |
| 101111 | XLVII |
| 110000 | XLVIII |
| 110001 | XLIX |
| 110010 | L |
| 110011 | LI |
| 110100 | LII |
| 110101 | LIII |
| 110110 | LIV |
| 110111 | LV |
| 111000 | LVI |
| 111001 | LVII |
| 111010 | LVIII |
| 111011 | LIX |
| 111100 | LX |
| 111101 | LXI |
| 111110 | LXII |
| 111111 | LXIII |
| 1000000 | LXIV |
| 1000001 | LXV |
| 1000010 | LXVI |
| 1000011 | LXVII |
| 1000100 | LXVIII |
| 1000101 | LXIX |
| 1000110 | LXX |
| 1000111 | LXXI |
| 1001000 | LXXII |
| 1001001 | LXXIII |
| 1001010 | LXXIV |
| 1001011 | LXXV |
| 1001100 | LXXVI |
| 1001101 | LXXVII |
| 1001110 | LXXVIII |
| 1001111 | LXXIX |
| 1010000 | LXXX |
| 1010001 | LXXXI |
| 1010010 | LXXXII |
| 1010011 | LXXXIII |
| 1010100 | LXXXIV |
| 1010101 | LXXXV |
| 1010110 | LXXXVI |
| 1010111 | LXXXVII |
| 1011000 | LXXXVIII |
| 1011001 | LXXXIX |
| 1011010 | XC |
| 1011011 | XCI |
| 1011100 | XCII |
| 1011101 | XCIII |
| 1011110 | XCIV |
| 1011111 | XCV |
| 1100000 | XCVI |
| 1100001 | XCVII |
| 1100010 | XCVIII |
| 1100011 | XCIX |
| 1100100 | C |
| 1100101 | CI |
| 1100110 | CII |
| 1100111 | CIII |
| 1101000 | CIV |
| 1101001 | CV |
| 1101010 | CVI |
| 1101011 | CVII |
| 1101100 | CVIII |
| 1101101 | CIX |
| 1101110 | CX |
| 1101111 | CXI |
| 1110000 | CXII |
| 1110001 | CXIII |
| 1110010 | CXIV |
| 1110011 | CXV |
| 1110100 | CXVI |
| 1110101 | CXVII |
| 1110110 | CXVIII |
| 1110111 | CXIX |
| 1111000 | CXX |
| 1111001 | CXXI |
| 1111010 | CXXII |
| 1111011 | CXXIII |
| 1111100 | CXXIV |
| 1111101 | CXXV |
| 1111110 | CXXVI |
| 1111111 | CXXVII |
| 10000000 | CXXVIII |
| 10000001 | CXXIX |
| 10000010 | CXXX |
| 10000011 | CXXXI |
| 10000100 | CXXXII |
| 10000101 | CXXXIII |
| 10000110 | CXXXIV |
| 10000111 | CXXXV |
| 10001000 | CXXXVI |
| 10001001 | CXXXVII |
| 10001010 | CXXXVIII |
| 10001011 | CXXXIX |
| 10001100 | CXL |
| 10001101 | CXLI |
| 10001110 | CXLII |
| 10001111 | CXLIII |
| 10010000 | CXLIV |
| 10010001 | CXLV |
| 10010010 | CXLVI |
| 10010011 | CXLVII |
| 10010100 | CXLVIII |
| 10010101 | CXLIX |
| 10010110 | CL |
| 10010111 | CLI |
| 10011000 | CLII |
| 10011001 | CLIII |
| 10011010 | CLIV |
| 10011011 | CLV |
| 10011100 | CLVI |
| 10011101 | CLVII |
| 10011110 | CLVIII |
| 10011111 | CLIX |
| 10100000 | CLX |
| 10100001 | CLXI |
| 10100010 | CLXII |
| 10100011 | CLXIII |
| 10100100 | CLXIV |
| 10100101 | CLXV |
| 10100110 | CLXVI |
| 10100111 | CLXVII |
| 10101000 | CLXVIII |
| 10101001 | CLXIX |
| 10101010 | CLXX |
| 10101011 | CLXXI |
| 10101100 | CLXXII |
| 10101101 | CLXXIII |
| 10101110 | CLXXIV |
| 10101111 | CLXXV |
| 10110000 | CLXXVI |
| 10110001 | CLXXVII |
| 10110010 | CLXXVIII |
| 10110011 | CLXXIX |
| 10110100 | CLXXX |
| 10110101 | CLXXXI |
| 10110110 | CLXXXII |
| 10110111 | CLXXXIII |
| 10111000 | CLXXXIV |
| 10111001 | CLXXXV |
| 10111010 | CLXXXVI |
| 10111011 | CLXXXVII |
| 10111100 | CLXXXVIII |
| 10111101 | CLXXXIX |
| 10111110 | CXC |
| 10111111 | CXCI |
| 11000000 | CXCII |
| 11000001 | CXCIII |
| 11000010 | CXCIV |
| 11000011 | CXCV |
| 11000100 | CXCVI |
| 11000101 | CXCVII |
| 11000110 | CXCVIII |
| 11000111 | CXCIX |
| 11001000 | CC |
| 11001001 | CCI |
| 11001010 | CCII |
| 11001011 | CCIII |
| 11001100 | CCIV |
| 11001101 | CCV |
| 11001110 | CCVI |
| 11001111 | CCVII |
| 11010000 | CCVIII |
| 11010001 | CCIX |
| 11010010 | CCX |
| 11010011 | CCXI |
| 11010100 | CCXII |
| 11010101 | CCXIII |
| 11010110 | CCXIV |
| 11010111 | CCXV |
| 11011000 | CCXVI |
| 11011001 | CCXVII |
| 11011010 | CCXVIII |
| 11011011 | CCXIX |
| 11011100 | CCXX |
| 11011101 | CCXXI |
| 11011110 | CCXXII |
| 11011111 | CCXXIII |
| 11100000 | CCXXIV |
| 11100001 | CCXXV |
| 11100010 | CCXXVI |
| 11100011 | CCXXVII |
| 11100100 | CCXXVIII |
| 11100101 | CCXXIX |
| 11100110 | CCXXX |
| 11100111 | CCXXXI |
| 11101000 | CCXXXII |
| 11101001 | CCXXXIII |
| 11101010 | CCXXXIV |
| 11101011 | CCXXXV |
| 11101100 | CCXXXVI |
| 11101101 | CCXXXVII |
| 11101110 | CCXXXVIII |
| 11101111 | CCXXXIX |
| 11110000 | CCXL |
| 11110001 | CCXLI |
| 11110010 | CCXLII |
| 11110011 | CCXLIII |
| 11110100 | CCXLIV |
| 11110101 | CCXLV |
| 11110110 | CCXLVI |
| 11110111 | CCXLVII |
| 11111000 | CCXLVIII |
| 11111001 | CCXLIX |
| 11111010 | CCL |
| 11111011 | CCLI |
| 11111100 | CCLII |
| 11111101 | CCLIII |
| 11111110 | CCLIV |
| 11111111 | CCLV |
| 100000000 | CCLVI |
| 100000001 | CCLVII |
| 100000010 | CCLVIII |
| 100000011 | CCLIX |
| 100000100 | CCLX |
| 100000101 | CCLXI |
| 100000110 | CCLXII |
| 100000111 | CCLXIII |
| 100001000 | CCLXIV |
| 100001001 | CCLXV |
| 100001010 | CCLXVI |
| 100001011 | CCLXVII |
| 100001100 | CCLXVIII |
| 100001101 | CCLXIX |
| 100001110 | CCLXX |
| 100001111 | CCLXXI |
| 100010000 | CCLXXII |
| 100010001 | CCLXXIII |
| 100010010 | CCLXXIV |
| 100010011 | CCLXXV |
| 100010100 | CCLXXVI |
| 100010101 | CCLXXVII |
| 100010110 | CCLXXVIII |
| 100010111 | CCLXXIX |
| 100011000 | CCLXXX |
| 100011001 | CCLXXXI |
| 100011010 | CCLXXXII |
| 100011011 | CCLXXXIII |
| 100011100 | CCLXXXIV |
| 100011101 | CCLXXXV |
| 100011110 | CCLXXXVI |
| 100011111 | CCLXXXVII |
| 100100000 | CCLXXXVIII |
| 100100001 | CCLXXXIX |
| 100100010 | CCXC |
| 100100011 | CCXCI |
| 100100100 | CCXCII |
| 100100101 | CCXCIII |
| 100100110 | CCXCIV |
| 100100111 | CCXCV |
| 100101000 | CCXCVI |
| 100101001 | CCXCVII |
| 100101010 | CCXCVIII |
| 100101011 | CCXCIX |
| 100101100 | CCC |