Konvertieren von Oktal (Basis 8) zu Binär (Basis 2)
Führen Sie die Umrechnung von Zahlen zwischen verschiedenen Zahlensystemen durch.
Oktal (Basis 8) = Binär (Basis 2)
Informationen über Konvertierungseinheiten:
Über Oktal (Basis 8)
Das Oktalsystem ist ein Stellenwertsystem mit der Basis 8, das die arabisch-indischen Ziffern verwendet: 0,1,2,3,4,5,6,7. In der Informatik wird manchmal die Oktalzahl anstelle der Hexadezimalzahl verwendet. Ein Vorteil ist, dass keine anderen Symbole außer den Ziffern verwendet werden müssen.
Über Binär (Basis 2)
Das Binärsystem ist eine Zähltechnik, die nur zwei Ziffern verwendet, nämlich 0 und 1. Es wird häufig in der Informatik verwendet. Diese Methode beruht ausschließlich auf zwei Symbolen, der Eins und der Null. Jede Zahl kann sowohl im Dezimalsystem als auch im Binärsystem ausgedrückt werden.
Oktal (Basis 8) vs Binär (Basis 2)
| Oktal (Basis 8) | Binär (Basis 2) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
¿Wie man von Oktal (Basis 8) zu Binär (Basis 2)?
Hinweis: Um eine Oktalzahl (Basis 8) in eine andere Basis zu konvertieren, muss sie zuerst in eine Dezimalzahl (Basis 10) umgerechnet werden. Folgen Sie diesen Schritten:
- Identifizieren Sie jede Ziffer der Oktalzahl.
- Berechnen Sie die Position jeder Ziffer. Beginnen Sie von der rechten Seite, wobei die rechteste Ziffer die Position 0 hat. Jede weitere Ziffer nach links erhält eine um 1 erhöhte Position (1, 2, 3 usw.).
- Berechnen Sie den Dezimalwert jeder Ziffer, indem Sie sie mit der Basis (8) hoch der Position der Ziffer multiplizieren. Zum Beispiel: Ziffer * 8^Position.
- Summieren Sie die erhaltenen Werte aus dem vorherigen Schritt, um die äquivalente Dezimalzahl zu erhalten.
Anwendung dieser Schritte auf die Oktalzahl 237:
- 2, 3 und 7 sind die Ziffern.
- Ausgehend von rechts sind die Positionen 0, 1 und 2.
- 2 * 8^2 = 128; 3 * 8^1 = 24; 7 * 8^0 = 7.
- 128 + 24 + 7 = 159 dezimal
Also gilt: 237 oktal = 159 dezimal.

Hinweis: Um eine Dezimalzahl (Basis 10) in eine Binärzahl (Basis 2) umzuwandeln, befolgen Sie diese Schritte:
- Teilen Sie die Dezimalzahl wiederholt durch 2 und notieren Sie die Reste der Divisionen.
- Der Vorgang endet, wenn das Ergebnis der Division gleich 0 ist.
- Die Reste der Divisionen müssen in umgekehrter Reihenfolge geschrieben werden, da sie die Gewichte der entsprechenden binären Ziffern darstellen.
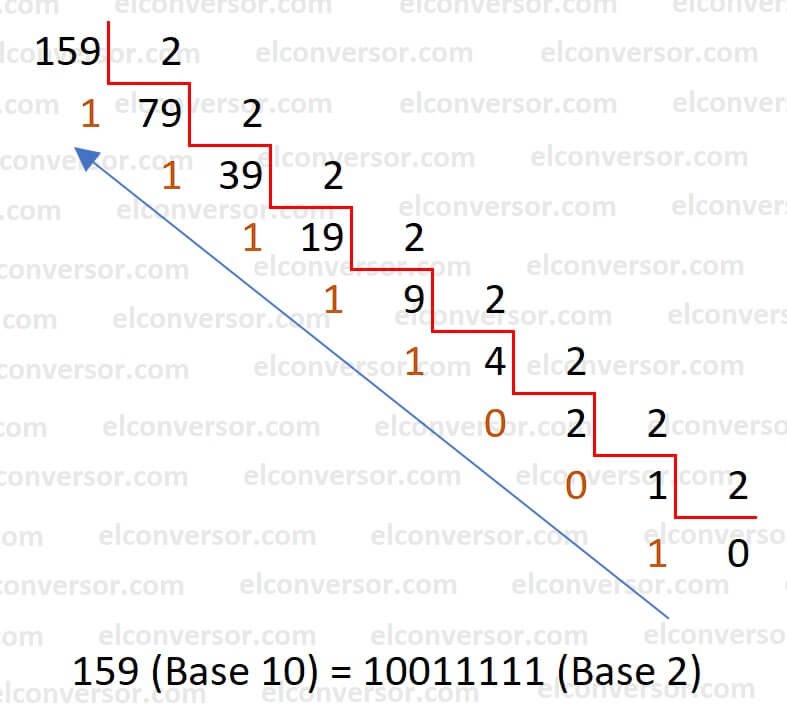
Anwendung dieser Schritte auf die Dezimalzahl 159:
Hier ist ein Beispiel, wie man die Dezimalzahl 159 in binär umwandelt:
- Teilen Sie 159 durch 2: 159 ÷ 2 = 79 mit einem Rest von 1.
- Teilen Sie 79 durch 2: 79 ÷ 2 = 39 mit einem Rest von 1.
- Teilen Sie 39 durch 2: 39 ÷ 2 = 19 mit einem Rest von 1.
- Teilen Sie 19 durch 2: 19 ÷ 2 = 9 mit einem Rest von 1.
- Teilen Sie 9 durch 2: 9 ÷ 2 = 4 mit einem Rest von 1.
- Teilen Sie 4 durch 2: 4 ÷ 2 = 2 mit einem Rest von 0.
- Teilen Sie 2 durch 2: 2 ÷ 2 = 1 mit einem Rest von 0.
- Teilen Sie 1 durch 2: 1 ÷ 2 = 0 mit einem Rest von 1.
Die Reste der Divisionen werden in umgekehrter Reihenfolge geschrieben: 10011111.
Also wird die Dezimalzahl 159 in binär zu 10011111.
Konversionstabelle von Oktal (Basis 8) zu Binär (Basis 2)
| Oktal (Basis 8) | Binär (Basis 2) |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 10 | 1000 |
| 11 | 1001 |
| 12 | 1010 |
| 13 | 1011 |
| 14 | 1100 |
| 15 | 1101 |
| 16 | 1110 |
| 17 | 1111 |
| 20 | 10000 |
| 21 | 10001 |
| 22 | 10010 |
| 23 | 10011 |
| 24 | 10100 |
| 25 | 10101 |
| 26 | 10110 |
| 27 | 10111 |
| 30 | 11000 |
| 31 | 11001 |
| 32 | 11010 |
| 33 | 11011 |
| 34 | 11100 |
| 35 | 11101 |
| 36 | 11110 |
| 37 | 11111 |
| 40 | 100000 |
| 41 | 100001 |
| 42 | 100010 |
| 43 | 100011 |
| 44 | 100100 |
| 45 | 100101 |
| 46 | 100110 |
| 47 | 100111 |
| 50 | 101000 |
| 51 | 101001 |
| 52 | 101010 |
| 53 | 101011 |
| 54 | 101100 |
| 55 | 101101 |
| 56 | 101110 |
| 57 | 101111 |
| 60 | 110000 |
| 61 | 110001 |
| 62 | 110010 |
| 63 | 110011 |
| 64 | 110100 |
| 65 | 110101 |
| 66 | 110110 |
| 67 | 110111 |
| 70 | 111000 |
| 71 | 111001 |
| 72 | 111010 |
| 73 | 111011 |
| 74 | 111100 |
| 75 | 111101 |
| 76 | 111110 |
| 77 | 111111 |
| 100 | 1000000 |
| 101 | 1000001 |
| 102 | 1000010 |
| 103 | 1000011 |
| 104 | 1000100 |
| 105 | 1000101 |
| 106 | 1000110 |
| 107 | 1000111 |
| 110 | 1001000 |
| 111 | 1001001 |
| 112 | 1001010 |
| 113 | 1001011 |
| 114 | 1001100 |
| 115 | 1001101 |
| 116 | 1001110 |
| 117 | 1001111 |
| 120 | 1010000 |
| 121 | 1010001 |
| 122 | 1010010 |
| 123 | 1010011 |
| 124 | 1010100 |
| 125 | 1010101 |
| 126 | 1010110 |
| 127 | 1010111 |
| 130 | 1011000 |
| 131 | 1011001 |
| 132 | 1011010 |
| 133 | 1011011 |
| 134 | 1011100 |
| 135 | 1011101 |
| 136 | 1011110 |
| 137 | 1011111 |
| 140 | 1100000 |
| 141 | 1100001 |
| 142 | 1100010 |
| 143 | 1100011 |
| 144 | 1100100 |
| 145 | 1100101 |
| 146 | 1100110 |
| 147 | 1100111 |
| 150 | 1101000 |
| 151 | 1101001 |
| 152 | 1101010 |
| 153 | 1101011 |
| 154 | 1101100 |
| 155 | 1101101 |
| 156 | 1101110 |
| 157 | 1101111 |
| 160 | 1110000 |
| 161 | 1110001 |
| 162 | 1110010 |
| 163 | 1110011 |
| 164 | 1110100 |
| 165 | 1110101 |
| 166 | 1110110 |
| 167 | 1110111 |
| 170 | 1111000 |
| 171 | 1111001 |
| 172 | 1111010 |
| 173 | 1111011 |
| 174 | 1111100 |
| 175 | 1111101 |
| 176 | 1111110 |
| 177 | 1111111 |
| 200 | 10000000 |
| 201 | 10000001 |
| 202 | 10000010 |
| 203 | 10000011 |
| 204 | 10000100 |
| 205 | 10000101 |
| 206 | 10000110 |
| 207 | 10000111 |
| 210 | 10001000 |
| 211 | 10001001 |
| 212 | 10001010 |
| 213 | 10001011 |
| 214 | 10001100 |
| 215 | 10001101 |
| 216 | 10001110 |
| 217 | 10001111 |
| 220 | 10010000 |
| 221 | 10010001 |
| 222 | 10010010 |
| 223 | 10010011 |
| 224 | 10010100 |
| 225 | 10010101 |
| 226 | 10010110 |
| 227 | 10010111 |
| 230 | 10011000 |
| 231 | 10011001 |
| 232 | 10011010 |
| 233 | 10011011 |
| 234 | 10011100 |
| 235 | 10011101 |
| 236 | 10011110 |
| 237 | 10011111 |
| 240 | 10100000 |
| 241 | 10100001 |
| 242 | 10100010 |
| 243 | 10100011 |
| 244 | 10100100 |
| 245 | 10100101 |
| 246 | 10100110 |
| 247 | 10100111 |
| 250 | 10101000 |
| 251 | 10101001 |
| 252 | 10101010 |
| 253 | 10101011 |
| 254 | 10101100 |
| 255 | 10101101 |
| 256 | 10101110 |
| 257 | 10101111 |
| 260 | 10110000 |
| 261 | 10110001 |
| 262 | 10110010 |
| 263 | 10110011 |
| 264 | 10110100 |
| 265 | 10110101 |
| 266 | 10110110 |
| 267 | 10110111 |
| 270 | 10111000 |
| 271 | 10111001 |
| 272 | 10111010 |
| 273 | 10111011 |
| 274 | 10111100 |
| 275 | 10111101 |
| 276 | 10111110 |
| 277 | 10111111 |
| 300 | 11000000 |
| 301 | 11000001 |
| 302 | 11000010 |
| 303 | 11000011 |
| 304 | 11000100 |
| 305 | 11000101 |
| 306 | 11000110 |
| 307 | 11000111 |
| 310 | 11001000 |
| 311 | 11001001 |
| 312 | 11001010 |
| 313 | 11001011 |
| 314 | 11001100 |
| 315 | 11001101 |
| 316 | 11001110 |
| 317 | 11001111 |
| 320 | 11010000 |
| 321 | 11010001 |
| 322 | 11010010 |
| 323 | 11010011 |
| 324 | 11010100 |
| 325 | 11010101 |
| 326 | 11010110 |
| 327 | 11010111 |
| 330 | 11011000 |
| 331 | 11011001 |
| 332 | 11011010 |
| 333 | 11011011 |
| 334 | 11011100 |
| 335 | 11011101 |
| 336 | 11011110 |
| 337 | 11011111 |
| 340 | 11100000 |
| 341 | 11100001 |
| 342 | 11100010 |
| 343 | 11100011 |
| 344 | 11100100 |
| 345 | 11100101 |
| 346 | 11100110 |
| 347 | 11100111 |
| 350 | 11101000 |
| 351 | 11101001 |
| 352 | 11101010 |
| 353 | 11101011 |
| 354 | 11101100 |
| 355 | 11101101 |
| 356 | 11101110 |
| 357 | 11101111 |
| 360 | 11110000 |
| 361 | 11110001 |
| 362 | 11110010 |
| 363 | 11110011 |
| 364 | 11110100 |
| 365 | 11110101 |
| 366 | 11110110 |
| 367 | 11110111 |
| 370 | 11111000 |
| 371 | 11111001 |
| 372 | 11111010 |
| 373 | 11111011 |
| 374 | 11111100 |
| 375 | 11111101 |
| 376 | 11111110 |
| 377 | 11111111 |
| 400 | 100000000 |
| 401 | 100000001 |
| 402 | 100000010 |
| 403 | 100000011 |
| 404 | 100000100 |
| 405 | 100000101 |
| 406 | 100000110 |
| 407 | 100000111 |
| 410 | 100001000 |
| 411 | 100001001 |
| 412 | 100001010 |
| 413 | 100001011 |
| 414 | 100001100 |
| 415 | 100001101 |
| 416 | 100001110 |
| 417 | 100001111 |
| 420 | 100010000 |
| 421 | 100010001 |
| 422 | 100010010 |
| 423 | 100010011 |
| 424 | 100010100 |
| 425 | 100010101 |
| 426 | 100010110 |
| 427 | 100010111 |
| 430 | 100011000 |
| 431 | 100011001 |
| 432 | 100011010 |
| 433 | 100011011 |
| 434 | 100011100 |
| 435 | 100011101 |
| 436 | 100011110 |
| 437 | 100011111 |
| 440 | 100100000 |
| 441 | 100100001 |
| 442 | 100100010 |
| 443 | 100100011 |
| 444 | 100100100 |
| 445 | 100100101 |
| 446 | 100100110 |
| 447 | 100100111 |
| 450 | 100101000 |
| 451 | 100101001 |
| 452 | 100101010 |
| 453 | 100101011 |
| 454 | 100101100 |