Konvertieren von Binär (Basis 2) zu Hexadezimal (Basis 16)
Führen Sie die Umrechnung von Zahlen zwischen verschiedenen Zahlensystemen durch.
Binär (Basis 2) = Hexadezimal (Basis 16)
Informationen über Konvertierungseinheiten:
Über Binär (Basis 2)
Das Binärsystem ist eine Zähltechnik, die nur zwei Ziffern verwendet, nämlich 0 und 1. Es wird häufig in der Informatik verwendet. Diese Methode beruht ausschließlich auf zwei Symbolen, der Eins und der Null. Jede Zahl kann sowohl im Dezimalsystem als auch im Binärsystem ausgedrückt werden.
Über Hexadezimal (Basis 16)
Das hexadezimale System reduziert eine achtköpfige Zahl auf nur zwei hexadezimale Ziffern. Dies verringert die Verwirrung, die beim Lesen langer Zeichenfolgen von Binärzahlen auftreten kann, sowie den Platzbedarf für das Schreiben von Binärzahlen.
Binär (Basis 2) vs Hexadezimal (Basis 16)
| Binär (Basis 2) | Hexadezimal (Basis 16) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | a |
| 1011 | b |
| 1100 | c |
| 1101 | d |
| 1110 | e |
| 1111 | f |
¿Wie man von Binär (Basis 2) zu Hexadezimal (Basis 16)?
Hinweis: Um eine Zahl im Binärsystem (Basis 2) in jede andere Basis umzuwandeln, müssen wir zuerst den binären Wert in das Dezimalsystem (Basis 10) umrechnen. Befolgen Sie diese Schritte:
- Identifizieren Sie jede Ziffer der binären Zahl.
- Berechnen Sie die Position jeder Ziffer. Beginnen Sie von der rechtesten Ziffer, die die Position 0 haben wird. Jede Ziffer links davon erhält eine inkrementelle Position von 1 (1, 2, 3 usw.).
- Berechnen Sie den dezimalen Wert jeder Ziffer, indem Sie sie mit der Basis (2) hoch zur Position der Ziffer multiplizieren. Zum Beispiel: Ziffer * 2^Position.
- Addieren Sie die Werte aus dem vorherigen Schritt, um die äquivalente Dezimalzahl zu erhalten.
Anwendung dieser Schritte auf die binäre Zahl 10011111:
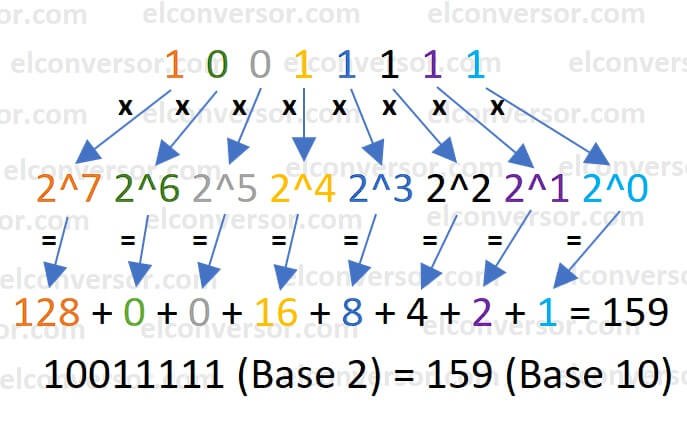
Schauen wir uns an, wie man die binäre Zahl 10011111 in Dezimal umrechnet.
- 1, 0, 0, 1, 1, 1, 1 und 1 sind die Ziffern.
- Beginnend von rechts sind die Positionen 0, 1, 2, 3, 4, 5, 6 und 7.
- 1 * 2^7 = 128; 0 * 2^6 = 0; 0 * 2^5 = 0; 1 * 2^4 = 16; 1 * 2^3 = 8; 1 * 2^2 = 4; 1 * 2^1 = 2; 1 * 2^0 = 1;
- 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159 dezimal.
Also, 10011111 binär = 159 dezimal.
Um eine dezimale Zahl (Basis 10) in hexadezimal (Basis 16) umzuwandeln, befolgen Sie diese Schritte:
- Teilen Sie die dezimale Zahl durch 16.
- Nehmen Sie den Quotienten und teilen Sie ihn erneut durch 16.
- Wiederholen Sie diesen Vorgang, bis der Quotient kleiner als 16 ist.
- Weisen Sie jedem Rest einen Buchstaben zu, wenn der Rest größer als 9 ist.
- Die Zahlen 10, 11, 12, 13, 14 und 15 werden durch die Buchstaben A, B, C, D, E und F repräsentiert.
- Schreiben Sie die erhaltenen Reste in umgekehrter Reihenfolge auf, in der sie berechnet wurden.
Anwendung dieser Schritte auf die dezimale Zahl 159:
- 159 / 16 = 9 mit einem Rest von 15.
- 9 / 16 = 0 mit einem Rest von 9.
- 15 wird als F dargestellt.
- 9 wird als 9 dargestellt.

Konversionstabelle von Binär (Basis 2) zu Hexadezimal (Basis 16)
| Binär (Basis 2) | Hexadezimal (Basis 16) |
|---|---|
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | a |
| 1011 | b |
| 1100 | c |
| 1101 | d |
| 1110 | e |
| 1111 | f |
| 10000 | 10 |
| 10001 | 11 |
| 10010 | 12 |
| 10011 | 13 |
| 10100 | 14 |
| 10101 | 15 |
| 10110 | 16 |
| 10111 | 17 |
| 11000 | 18 |
| 11001 | 19 |
| 11010 | 1a |
| 11011 | 1b |
| 11100 | 1c |
| 11101 | 1d |
| 11110 | 1e |
| 11111 | 1f |
| 100000 | 20 |
| 100001 | 21 |
| 100010 | 22 |
| 100011 | 23 |
| 100100 | 24 |
| 100101 | 25 |
| 100110 | 26 |
| 100111 | 27 |
| 101000 | 28 |
| 101001 | 29 |
| 101010 | 2a |
| 101011 | 2b |
| 101100 | 2c |
| 101101 | 2d |
| 101110 | 2e |
| 101111 | 2f |
| 110000 | 30 |
| 110001 | 31 |
| 110010 | 32 |
| 110011 | 33 |
| 110100 | 34 |
| 110101 | 35 |
| 110110 | 36 |
| 110111 | 37 |
| 111000 | 38 |
| 111001 | 39 |
| 111010 | 3a |
| 111011 | 3b |
| 111100 | 3c |
| 111101 | 3d |
| 111110 | 3e |
| 111111 | 3f |
| 1000000 | 40 |
| 1000001 | 41 |
| 1000010 | 42 |
| 1000011 | 43 |
| 1000100 | 44 |
| 1000101 | 45 |
| 1000110 | 46 |
| 1000111 | 47 |
| 1001000 | 48 |
| 1001001 | 49 |
| 1001010 | 4a |
| 1001011 | 4b |
| 1001100 | 4c |
| 1001101 | 4d |
| 1001110 | 4e |
| 1001111 | 4f |
| 1010000 | 50 |
| 1010001 | 51 |
| 1010010 | 52 |
| 1010011 | 53 |
| 1010100 | 54 |
| 1010101 | 55 |
| 1010110 | 56 |
| 1010111 | 57 |
| 1011000 | 58 |
| 1011001 | 59 |
| 1011010 | 5a |
| 1011011 | 5b |
| 1011100 | 5c |
| 1011101 | 5d |
| 1011110 | 5e |
| 1011111 | 5f |
| 1100000 | 60 |
| 1100001 | 61 |
| 1100010 | 62 |
| 1100011 | 63 |
| 1100100 | 64 |
| 1100101 | 65 |
| 1100110 | 66 |
| 1100111 | 67 |
| 1101000 | 68 |
| 1101001 | 69 |
| 1101010 | 6a |
| 1101011 | 6b |
| 1101100 | 6c |
| 1101101 | 6d |
| 1101110 | 6e |
| 1101111 | 6f |
| 1110000 | 70 |
| 1110001 | 71 |
| 1110010 | 72 |
| 1110011 | 73 |
| 1110100 | 74 |
| 1110101 | 75 |
| 1110110 | 76 |
| 1110111 | 77 |
| 1111000 | 78 |
| 1111001 | 79 |
| 1111010 | 7a |
| 1111011 | 7b |
| 1111100 | 7c |
| 1111101 | 7d |
| 1111110 | 7e |
| 1111111 | 7f |
| 10000000 | 80 |
| 10000001 | 81 |
| 10000010 | 82 |
| 10000011 | 83 |
| 10000100 | 84 |
| 10000101 | 85 |
| 10000110 | 86 |
| 10000111 | 87 |
| 10001000 | 88 |
| 10001001 | 89 |
| 10001010 | 8a |
| 10001011 | 8b |
| 10001100 | 8c |
| 10001101 | 8d |
| 10001110 | 8e |
| 10001111 | 8f |
| 10010000 | 90 |
| 10010001 | 91 |
| 10010010 | 92 |
| 10010011 | 93 |
| 10010100 | 94 |
| 10010101 | 95 |
| 10010110 | 96 |
| 10010111 | 97 |
| 10011000 | 98 |
| 10011001 | 99 |
| 10011010 | 9a |
| 10011011 | 9b |
| 10011100 | 9c |
| 10011101 | 9d |
| 10011110 | 9e |
| 10011111 | 9f |
| 10100000 | a0 |
| 10100001 | a1 |
| 10100010 | a2 |
| 10100011 | a3 |
| 10100100 | a4 |
| 10100101 | a5 |
| 10100110 | a6 |
| 10100111 | a7 |
| 10101000 | a8 |
| 10101001 | a9 |
| 10101010 | aa |
| 10101011 | ab |
| 10101100 | ac |
| 10101101 | ad |
| 10101110 | ae |
| 10101111 | af |
| 10110000 | b0 |
| 10110001 | b1 |
| 10110010 | b2 |
| 10110011 | b3 |
| 10110100 | b4 |
| 10110101 | b5 |
| 10110110 | b6 |
| 10110111 | b7 |
| 10111000 | b8 |
| 10111001 | b9 |
| 10111010 | ba |
| 10111011 | bb |
| 10111100 | bc |
| 10111101 | bd |
| 10111110 | be |
| 10111111 | bf |
| 11000000 | c0 |
| 11000001 | c1 |
| 11000010 | c2 |
| 11000011 | c3 |
| 11000100 | c4 |
| 11000101 | c5 |
| 11000110 | c6 |
| 11000111 | c7 |
| 11001000 | c8 |
| 11001001 | c9 |
| 11001010 | ca |
| 11001011 | cb |
| 11001100 | cc |
| 11001101 | cd |
| 11001110 | ce |
| 11001111 | cf |
| 11010000 | d0 |
| 11010001 | d1 |
| 11010010 | d2 |
| 11010011 | d3 |
| 11010100 | d4 |
| 11010101 | d5 |
| 11010110 | d6 |
| 11010111 | d7 |
| 11011000 | d8 |
| 11011001 | d9 |
| 11011010 | da |
| 11011011 | db |
| 11011100 | dc |
| 11011101 | dd |
| 11011110 | de |
| 11011111 | df |
| 11100000 | e0 |
| 11100001 | e1 |
| 11100010 | e2 |
| 11100011 | e3 |
| 11100100 | e4 |
| 11100101 | e5 |
| 11100110 | e6 |
| 11100111 | e7 |
| 11101000 | e8 |
| 11101001 | e9 |
| 11101010 | ea |
| 11101011 | eb |
| 11101100 | ec |
| 11101101 | ed |
| 11101110 | ee |
| 11101111 | ef |
| 11110000 | f0 |
| 11110001 | f1 |
| 11110010 | f2 |
| 11110011 | f3 |
| 11110100 | f4 |
| 11110101 | f5 |
| 11110110 | f6 |
| 11110111 | f7 |
| 11111000 | f8 |
| 11111001 | f9 |
| 11111010 | fa |
| 11111011 | fb |
| 11111100 | fc |
| 11111101 | fd |
| 11111110 | fe |
| 11111111 | ff |
| 100000000 | 100 |
| 100000001 | 101 |
| 100000010 | 102 |
| 100000011 | 103 |
| 100000100 | 104 |
| 100000101 | 105 |
| 100000110 | 106 |
| 100000111 | 107 |
| 100001000 | 108 |
| 100001001 | 109 |
| 100001010 | 10a |
| 100001011 | 10b |
| 100001100 | 10c |
| 100001101 | 10d |
| 100001110 | 10e |
| 100001111 | 10f |
| 100010000 | 110 |
| 100010001 | 111 |
| 100010010 | 112 |
| 100010011 | 113 |
| 100010100 | 114 |
| 100010101 | 115 |
| 100010110 | 116 |
| 100010111 | 117 |
| 100011000 | 118 |
| 100011001 | 119 |
| 100011010 | 11a |
| 100011011 | 11b |
| 100011100 | 11c |
| 100011101 | 11d |
| 100011110 | 11e |
| 100011111 | 11f |
| 100100000 | 120 |
| 100100001 | 121 |
| 100100010 | 122 |
| 100100011 | 123 |
| 100100100 | 124 |
| 100100101 | 125 |
| 100100110 | 126 |
| 100100111 | 127 |
| 100101000 | 128 |
| 100101001 | 129 |
| 100101010 | 12a |
| 100101011 | 12b |
| 100101100 | 12c |